Area Ques 53
Question
- In what ratio, does the $X$-axis divide the area of the region bounded by the parabolas $y=4 x-x^{2}$ and $y=x^{2}-x ?$
$(1994,5$ M)
Show Answer
Answer:
Correct Answer: 53.$(121:4)$
Solution:
Formula:
- Given parabolas are $y=4 x-x^{2}$
and $ y=-(x-2)^{2}+4 $
or $ (x-2)^{2}=-(y-4) $
Therefore, it is a vertically downward parabola with vertex at $(2,4)$ and its axis is $x=2$
and
$ y=x^{2}-x \Rightarrow y=(x-\frac{1}{2})^2 \quad-\frac{1}{4} $
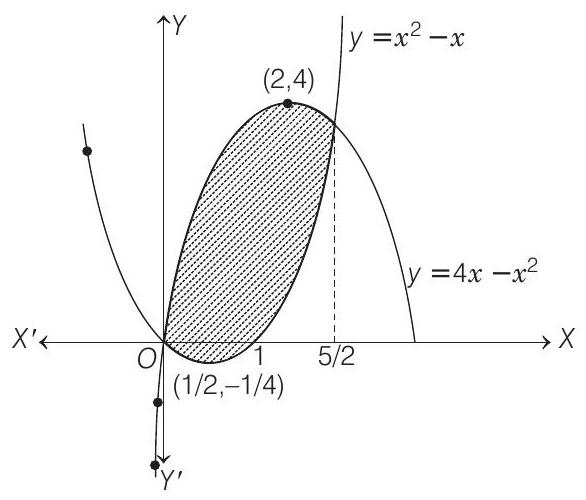
$ \Rightarrow \quad (x-\frac{1}{2})^{2}=y+\frac{1}{4} $
This is a parabola having its vertex at $(\frac{1}{2},-\frac{1}{4})$.
Its axis is at $x=\frac{1}{2}$ and opening upwards.
The points of intersection of given curves are
$ \begin{aligned} & 4 x-x^{2}=x^{2}-x \Rightarrow 2 x^{2}=5 x \\ & \Rightarrow \quad x(2-5 x)=0 \quad \Rightarrow \quad x=0, \frac{5}{2} \end{aligned} $
Also, $y=x^{2}-x$ meets $X$-axis at $(0,0)$ and $(1,0)$.
$\therefore$ Area, $A _{1}=\int _{0}^{5 / 2}\left[\left(4 x-x^{2}\right)-\left(x^{2}-x\right)\right] d x$
$ \begin{aligned} & =\int _{0}^{5 / 2}\left(5 x-2 x^{2}\right) d x \\ & =[\frac{5}{2} x^{2}-\frac{2}{3} x^{3}]{ } _{0}^{5 / 2}=\frac{5}{2} (\frac{5}{2})^{2}-\frac{2}{3} \cdot (\frac{5}{2})^{3} \\ & =\frac{5}{2} \cdot \frac{25}{4}-\frac{2}{3} \cdot \frac{125}{8} \\ & =\frac{125}{8} (1-\frac{2}{3})=\frac{125}{24} \text { sq units } \end{aligned} $
This area is considering above and below $X$-axis both. Now, for area below $X$-axis separately, we consider
$ A _{2}=-\int _{0}^{1}\left(x^{2}-x\right) d x=[\frac{x^{2}}{2}-\frac{x^{3}}{3}]{ } _{0}^{1}=\frac{1}{2}-\frac{1}{3}=\frac{1}{6} \text { sq units } $
Therefore, net area above the $X$-axis is
$ A _{1}-A _{2}=\frac{125-4}{24}=\frac{121}{24} \text { sq units } $
Hence, ratio of area above the $X$-axis and area below $X$-axis
$ =\frac{121}{24}: \frac{1}{6}=121: 4 $





