Area Ques 58
Question
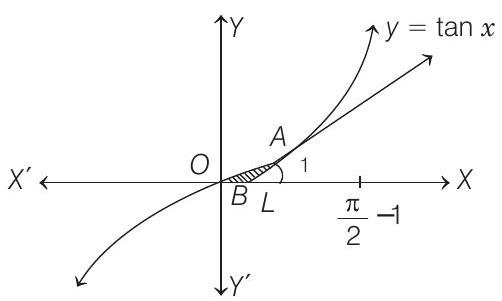
- Find the area of the region bounded by the curve $C: y=\tan x$, tangent drawn to $C$ at $x=\pi / 4$ and the $X$-axis.
$(1988,5 \mathrm{M})$
Show Answer
Answer:
Correct Answer: 58.$(\log \sqrt{2}-\frac{1}{4}) \text { sq unit }$
Solution:
Formula:
- Given, $y=\tan x \Rightarrow \frac{d y}{d x}=\sec ^{2} x$
$ \therefore \quad (\frac{d y}{d x}){ } _{x=\frac{\pi}{4}}=2 $
Hence, equation of tangent at $A (\frac{\pi}{4}, 1)$ is
$ \frac{y-1}{x-\pi / 4}=2 \Rightarrow y-1=2 x-\frac{\pi}{2} $
$ \Rightarrow \quad(2 x-y)=(\frac{\pi}{2}-1) $
$\therefore$ Required area is $O A B O$
$ \begin{aligned} & =\int _{0}^{\pi / 4}(\tan x) d x-\text { area of } \triangle A L B \\ & =[\log |\sec x|] _{0}^{\pi / 4}-\frac{1}{2} \cdot B L \cdot A L \\ & =\log \sqrt{2}-\frac{1}{2} (\frac{\pi}{4}-\frac{\pi-2}{4} ) \cdot 1 \\ & =(\log \sqrt{2}-\frac{1}{4}) \text { sq unit } \end{aligned} $





