Area Ques 59
Question
- Find the area bounded by the curves $x^{2}+y^{2}=25,4 y=\left|4-x^{2}\right|$ and $x=0$ above the $X$-axis.
$(1987,6 \mathrm{M})$
Show Answer
Answer:
Correct Answer: 59.$[4+25 \sin ^{-1} (\frac{4}{5})]$ sq units
Solution:
Formula:
- Given curves, $x^{2}+y^{2}=25,4 y=\left|4-x^{2}\right|$ could be sketched as below, whose points of intersection are
$ x^{2}+\frac{\left(4-x^{2}\right)^{2}}{16}=25 $
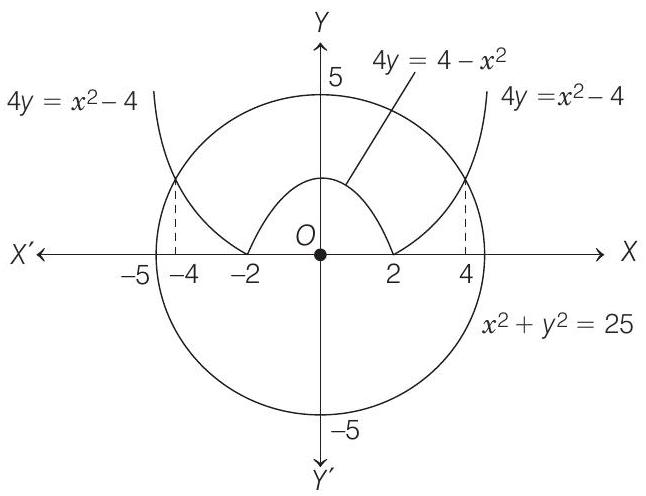
$ \Rightarrow \quad\left(x^{2}+24\right)\left(x^{2}-16\right)=0 $
$ \Rightarrow \quad x= \pm 4 $
$\therefore$ Required area $=2 [\int _{0}^{4} \sqrt{25-x^{2}} d x-\int _{0}^{2} (\frac{4-x^{2}}{4}) d x$ $-\int _{2}^{4} (\frac{x^{2}-4}{4}) d x ]$
$=2 \quad [[\frac{x}{2} \sqrt{25-x^{2}}+\frac{25}{2} \sin ^{-1} (\frac{x}{5}){ } _{0}^{4} ]$ $-\frac{1}{4} [4 x-\frac{x^{3}}{3}] { } _{0}^{2}-\frac{1}{4} [\frac{x^{3}}{3}-4 x] _{2}^{4}]$
$=2 \quad [[6+\frac{25}{2} \sin ^{-1} (\frac{4}{5}) ]-\frac{1}{4} [8-\frac{8}{3}]$ $ -\frac{1}{4} \quad [(\frac{64}{3}-16)-(\frac{8}{3}-8)]] $
$=2 \quad [6+\frac{25}{2} \sin ^{-1} (\frac{4}{5})-\frac{4}{3}-\frac{4}{3}-\frac{4}{3}]$
$=[4+25 \sin ^{-1} (\frac{4}{5})]$ sq units





