Area Ques 62
Question
- Sketch the region bounded by the curves $y=\sqrt{5-x^{2}}$ and $y=|x-1|$ and find its area.
(1985, 5M)
Show Answer
Answer:
Correct Answer: 62.$(\frac{5 \pi}{4}-\frac{1}{2})$ sq units
Solution:
Formula:
- Given curves $y=\sqrt{5-x^{2}}$ and $y=|x-1|$ could be sketched as shown, whose point of intersection are $5-x^{2}=(x-1)^{2}$
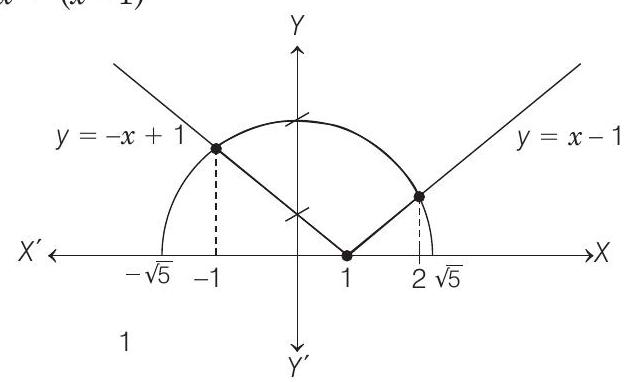
$\Rightarrow \quad 5-x^{2}=x^{2}-2 x+1$
$\Rightarrow \quad 2 x^{2}-2 x-4=0$ $\Rightarrow \quad x=2,-1$
$\therefore$ Required area
$=\int _{-1}^{2} \sqrt{5-x^{2}} d x-\int _{-1}^{1}(-x+1) d x-\int _{1}^{2}(x-1) d x$
$=[\frac{x}{2} \sqrt{5-x^{2}}+\frac{5}{2} \sin ^{-1} (\frac{x^{2}}{\sqrt{5}})]-[\frac{-x^{2}}{2}+x] _{-1}^{1}-[\frac{x^{2}}{2}-x] _{1}^{2}$
$=(1+\frac{5}{2} \sin ^{-1} \frac{2}{\sqrt{5}})-[-1+\frac{5}{2} \sin ^{-1} (\frac{-1}{\sqrt{5}})]$ $ -(-\frac{1}{2}+1+\frac{1}{2}+1)-(2-2-\frac{1}{2}+1) $
$=\frac{5}{2} (\sin ^{-1} \frac{2}{\sqrt{5}}+\sin ^{-1} \frac{1}{\sqrt{5}})-\frac{1}{2}$
$=\frac{5}{2} \sin ^{-1} (\frac{2}{\sqrt{5}} \sqrt{1-\frac{1}{5}}+\frac{1}{\sqrt{5}} \sqrt{1-\frac{4}{5}})-\frac{1}{2}$
$=\frac{5}{2} \sin ^{-1}(1)-\frac{1}{2}=(\frac{5 \pi}{4}-\frac{1}{2})$ sq units





