Area Ques 63
Question
- Find the area of the region bounded by the $X$-axis and the curves defined by $y=\tan x,-\frac{\pi}{3} \leq x \leq \frac{\pi}{3}$ and $y=\cot x, \frac{\pi}{6} \leq x \leq \frac{\pi}{3}$.
$(1984,4 M)$
Show Answer
Answer:
Correct Answer: 63.$(\frac{1}{2} \log _{e} 3)$ sq units
Solution:
Formula:
- Given, $y=\tan x,-\frac{\pi}{3} \leq x \leq \frac{\pi}{3}$
$\cot x, \quad \frac{\pi}{6} \leq x \leq \frac{\pi}{2}$
which could be plotted on the $Y$-axis.
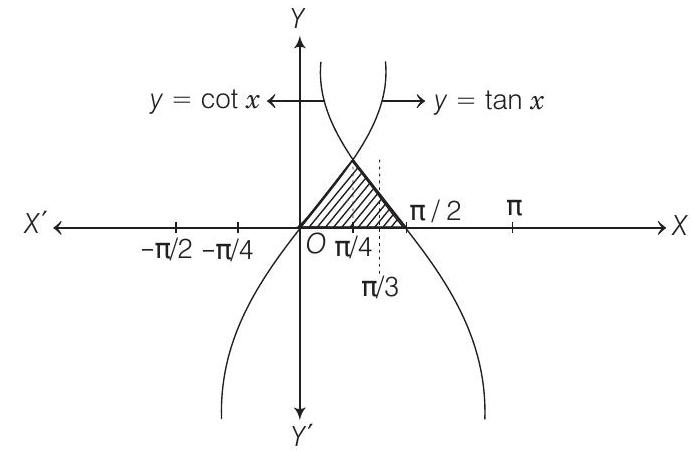
$\therefore$ Required area $=\int _{0}^{\pi / 4}(\tan x) d x+\int _{\pi / 4}^{\pi / 3}(\cot x) d x$
$=[-\log |\cos x|] _{0}^{\pi / 4}+[\log \sin x] _{\pi / 4}^{\pi / 3}$
$=-(\log \frac{1}{\sqrt{2}}-0)+(\log \frac{\sqrt{3}}{2}-\log \frac{1}{\sqrt{2}})$
$=\log \frac{\sqrt{3}}{2}-2 \log \frac{1}{\sqrt{2}}$
$=\log \frac{\sqrt{3}}{2}-\log \frac{1}{2}=\frac{1}{2} \log _{e} 3$ sq units





