Area Ques 66
Question
- For any real $t, x=\frac{e^{t}+e^{-t}}{2}, y=\frac{e^{t}-e^{-t}}{2}$ is a point on the hyperbola $x^{2}-y^{2}=1$. Find the area bounded by this hrperbola and the lines joining its centre to the points corresponding to $t _{1}$ and $-t _{1}$.
$(1982,3 \mathrm{M})$
Show Answer
Answer:
Correct Answer: 66.$(\frac{e^{2 t _{1}}-e^{-2 t _{1}}}{4}-\frac{1}{4}\left(e^{2 t _{1}}-e^{-2 t _{1}}-4 t _{1}\right))$
Solution:
Formula:
- Let $P=(\frac{e^{t _{1}}+e^{-t _{1}}}{2}, \frac{e^{t _{1}}-e^{-t _{1}}}{2})$
and $Q=(\frac{e^{-t}+e^{t _{1}}}{2}, \frac{e^{-t _{1}}-e^{t}}{2})$
We have to find the area of the region bounded by the curve $x^{2}-y^{2}=1$ and the lines joining the centre $x=0$, $y=0$ to the points $\left(t _{1}\right)$ and $\left(-t _{1}\right)$.
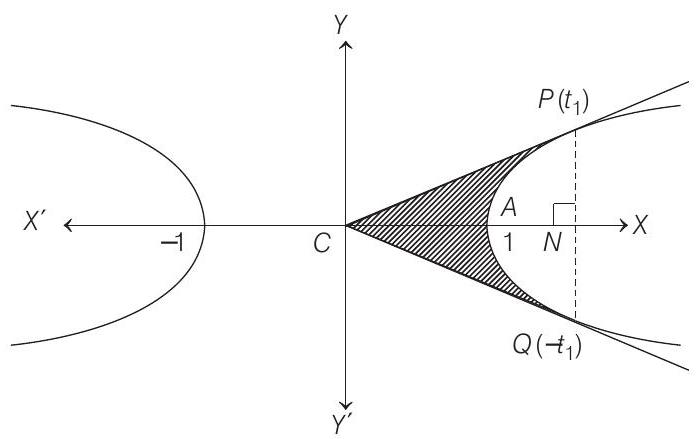
Required area
$ \begin{aligned} & =2 [\text { area of } \triangle P C N-\int _{1}^{\frac{e^{t _{1}}+e^{-t _{1}}}{2}}] y d x \\ & =2 [\frac{1}{2} (\frac{e^{t _{1}}+e^{-t _{1}}}{2}) (\frac{e^{t _{1}}-e^{-t _{1}}}{2})-\int _{1}^{t _{1}} y \frac{d y}{d t} \cdot d t] \\ & =2 [\frac{e^{2 t _{1}}-e^{-2 t _{1}}}{8}-\int _{0}^{t _{1}} \frac{e^{t}-e^{-t}}{2} d t] \\ & =\frac{e^{2 t _{1}}-e^{-2 t _{1}}}{4}-\frac{1}{2} \int _{0}^{t _{1}}\left(e^{2 t}+e^{-2 t}-2\right) d t \\ & =\frac{e^{2 t _{1}}-e^{-2 t _{1}}}{4}-\frac{1}{2} [\frac{e^{2 t}}{2}-\frac{e^{-2 t}}{2}-2 t] \\ & =\frac{e^{2 t _{1}}-e^{-2 t _{1}}}{4}-\frac{1}{4}\left(e^{2 t _{1}}-e^{-2 t _{1}}-4 t _{1}\right) \end{aligned} $





