Complex Numbers Ques 84
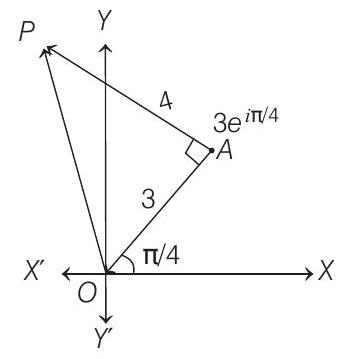
A man walks a distance of $3$ units from the origin towards the North-East ( $\left.N 45^{\circ} E\right)$ direction. From there, he walks a distance of $4$ units towards the North-West $\left(N 45^{\circ} W\right)$ direction to reach a point $P$. Then, the position of $P$ in the Argand plane is
(2007, 3M)
(a) $3 e^{i \pi / 4}+4 i$
(b) $(3-4 i) e^{i \pi / 4}$
(c) $(4+3 i) e^{i \pi / 4}$
(d) $(3+4 i) e^{i \pi / 4}$
Show Answer
Answer:
Correct Answer: 84.(d)
Solution:
Formula:
- Let $O A=3$, so that the complex number associated with $A$ is $3 e^{i \pi / 4}$.
If $z$ is the complex number associated with $P$, then
$\frac{z-3 e^{i \pi / 4}}{0-3 e^{i \pi / 4}} =\frac{4}{3} e^{-i \pi / 2}=-\frac{4 i}{3} $
$\Rightarrow \quad 3 z-9 e^{i \pi / 4} =12 i e^{i \pi / 4} $
$\Rightarrow \quad z =(3+4 i) e^{i \pi / 4}$