Functions Ques 22
If $S$ is the set of all real $x$ such that $\frac{2 x-1}{2 x^{3}+3 x^{2}+x}$ is positive, then $S$ contains
(1986, 2M)
(a) $(-\infty,-\frac{3}{2})$
(b) $(-\frac{3}{2},-\frac{1}{4})$
(c) $(-\frac{1}{4}, \frac{1}{2})$
(d) $(\frac{1}{2}, 3)$
Show Answer
Answer:
Correct Answer: 22.$(a, d)$
Solution:
Formula:
- Since,
$ \frac{2 x-1}{2 x^{3}+3 x^{2}+x}>0 $
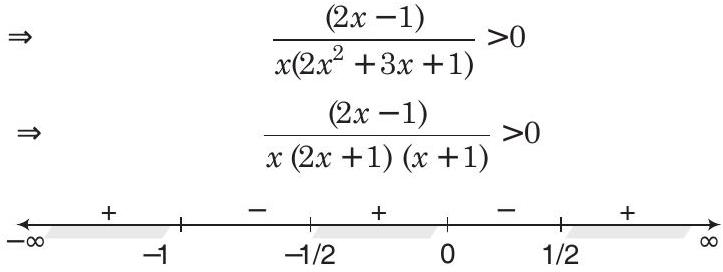
Hence, the solution set is,
$ x \in(-\infty,-1) \cup(-1 / 2,0) \cup(1 / 2, \infty) $
Hence, (a) and (d) are the correct options.





