Hyperbola Ques 9
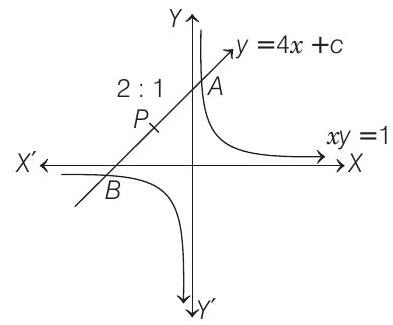
A variable straight line of slope 4 intersects the hyperbola $x y=1$ at two points. Find the locus of the point which divides the line segment between these two points in the ratio $1: 2$.
(1997, 5M)
Correct Answer: 9.($16 x^{2}+y^{2}+10 x y=2$) Solution: i.e. $A\left(t _1, 1 / t _1\right), B\left(t _2, 1 / t _2\right)$ $\therefore$ Coordinates of $P$ are $
(\frac{2 t _1+t _2}{2+1}, \frac{2 \cdot \frac{1}{t _1}+1 \cdot \frac{1}{t _2}}{2+1})=(h, k)
$ $\therefore h=\frac{2 t _1+t _2}{3}$ and $k=\frac{2 t _2+t _1}{3 t _1 t _2}$ $\quad$ …….(i) Also, $(t _1, \frac{1}{t _1})$ and $(t _2, \frac{1}{t _2})$ lie on $y=4 x+c$. $\Rightarrow \quad \frac{\frac{1}{t _2}-\frac{1}{t _1}}{t _2-t _1}=\frac{1}{t _1 t _2}=4 \quad$ or $\quad t _1 t _2=-1 / 4$ $\quad$ …….(ii) From Eq. (i), $t _1=2 h+\frac{k}{4}$ $
\text { and } \quad t _1=h-\frac{k}{2}
$ $\quad$ …….(iii) From Eqs. (ii) and (iii), $(-h-\frac{k}{2}) \quad (2 h+\frac{k}{4})=-\frac{1}{4}$ $
\begin{array}{lll}
\Rightarrow & (-\frac{2 h+k}{2}) \quad (\frac{8 h+k}{4})=-\frac{1}{4} \\
\Rightarrow & (2 h+k)(8 h+k)=2 \\
\Rightarrow & 16 h^{2}+k^{2}+10 h k=2
\end{array}
$ Hence, required locus is $16 x^{2}+y^{2}+10 x y=2$.Show Answer
Answer:
Formula: