Inverse Circular Functions Ques 23
- If $\alpha=\cos ^{-1} \frac{3}{5}, \beta=\tan ^{-1} \frac{1}{3}$, where $0<\alpha, \beta<\frac{\pi}{2}$, then $\alpha-\beta$ is equal to
(a) $\tan ^{-1} \frac{9}{5 \sqrt{10}}$
(b) $\cos ^{-1} \frac{9}{5 \sqrt{10}}$
(c) $\tan ^{-1} \frac{9}{14}$
(d) $\sin ^{-1} \frac{9}{5 \sqrt{10}}$
(2019 Main, 8 April I)
Show Answer
Answer:
Correct Answer: 23.(d)
Solution:
Formula:
Identities of Addition and Substraction:
- Given, $\alpha=\cos ^{-1} (\frac{3}{5})$ and $\beta=\tan ^{-1} (\frac{1}{3})$
where, $0<\alpha, \beta<\frac{\pi}{2}$
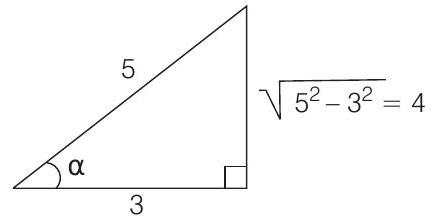
Clearly, $\alpha=\tan ^{-1} \frac{4}{3}$
So, $\alpha-\beta=\tan ^{-1} \frac{4}{3}-\tan ^{-1} \frac{1}{3}=\tan ^{-1} (\frac{\frac{4}{3}-\frac{1}{3}}{1+\frac{4}{3} \times \frac{1}{3}})$
$[\because \tan ^{-1} x-\tan ^{-1} y=\tan ^{-1} \frac{x-y}{1+x y}$, if $x y>-1]$
$=\tan ^{-1} \frac{1}{1+\frac{4}{9}}=\tan ^{-1} \frac{9}{13}$
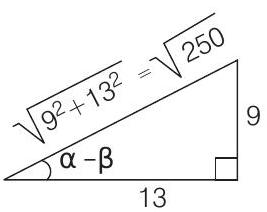
$=\sin ^{-1} \frac{9}{\sqrt{9^{2}+13^{2}}}=\sin ^{-1} \frac{9}{\sqrt{250}}$
$=\sin ^{-1} (\frac{9}{5 \sqrt{10}})$





