Probability Ques 118
A ball is drawn at random from box I and transferred to box II. If the probability of drawing a red ball from box I, after this transfer, is $\frac{1}{3}$, then the correct option(s) with the possible values of $n _1$ and $n _2$ is/are
(a) $n _1=4$ and $n _2=6$
(b) $n _1=2$ and $n _2=3$
(c) $n _1=10$ and $n _2=20$
(d) $n _1=3$ and $n _2=6$
Show Answer
Answer:
Correct Answer: 118.(d)
Solution:
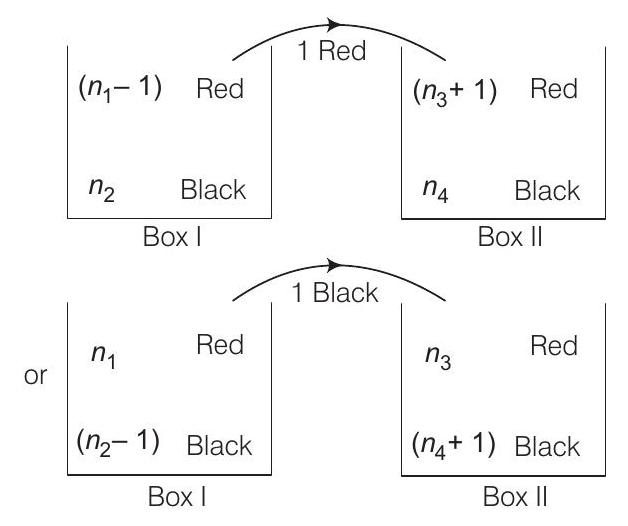
$\therefore P\left(\right.$ drawing red ball from $\left.B _1\right)=\frac{1}{3}$
$ \begin{aligned} & \Rightarrow (\frac{n _1-1}{n _1+n _2-1}) \quad (\frac{n _1}{n _1+n _2})+(\frac{n _2}{n _1+n _2}) \quad (\frac{n _1}{n _1+n _2-1})=\frac{1}{3} \\ & \Rightarrow \quad \frac{n _1^{2}+n _1 n _2-n _1}{\left(n _1+n _2\right)\left(n _1+n _2-1\right)}=\frac{1}{3} \end{aligned} $
Clearly, options (c) and (d) satisfy.





