Properties Of Triangles Ques 11
Let $A _1, A _2, \ldots, A _n$ be the vertices of an $n$-sided regular polygon such that $\frac{1}{A _1 A _2}=\frac{1}{A _1 A _3}+\frac{1}{A _1 A _4}$. Find the value of $n$.
$(1994,4$ M)
Show Answer
Answer:
Correct Answer: 11.($n=7$)
Solution:
- Let $O$ be the centre and $r$ be the radius of the circle passing through the vertices $A _1, A _2, \ldots, A _n$.
Then, $\quad \angle A _1 O A _2 =\frac{2 \pi}{n} $
also, $\quad O A _1 =O A _2=r$
Again, by cos formula, we know that,
$ \cos (\frac{2 \pi}{n})=\frac{O A _1^{2}+O A _2^{2}-A _1 A _2^{2}}{2\left(O A _1\right)\left(O A _2\right)} $
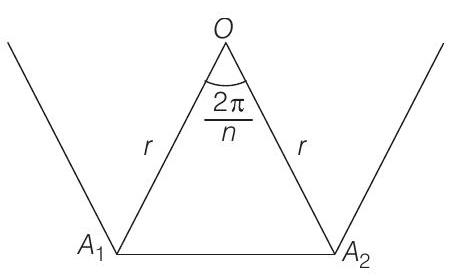
$ \begin{aligned} & \Rightarrow \quad \cos (\frac{2 \pi}{n})=\frac{r^{2}+r^{2}-A _1 A _2^{2}}{2(r)(r)} \\ & \Rightarrow \quad 2 r^{2} \cos (\frac{2 \pi}{n})=2 r^{2}-A _1 A _2^{2} \\ & \Rightarrow \quad A _1 A _2^{2}=2 r^{2}-2 r^{2} \cos (\frac{2 \pi}{n}) \\ & \Rightarrow \quad A _1 A _2^{2}=2 r^{2} [1-\cos (\frac{2 \pi}{n})] \\ & \Rightarrow \quad A _1 A _2^{2}=2 r^{2} \cdot 2 \sin ^{2} (\frac{\pi}{n}) \\ & \Rightarrow \quad A _1 A _2^{2}=4 r^{2} \sin ^{2} (\frac{\pi}{n}) \\ & \Rightarrow \quad A _1 A _2=2 r \sin \frac{\pi}{n} \\ & \text { Similarly, } \quad A _1 A _3=2 r \sin (\frac{2 \pi}{n}) \\ & \text { and } \quad A _1 A _4=2 r \sin (\frac{3 \pi}{n}) \\ & \text { Since, } \quad \frac{1}{A _1 A _2}=\frac{1}{A _1 A _3}+\frac{1}{A _1 A _4} \\ & \text { [given] } \\ & \Rightarrow \quad \frac{1}{2 r \sin (\pi / n)}=\frac{1}{2 r \sin (2 \pi / n)}+\frac{1}{2 r \sin (3 \pi / n)} \\ & \Rightarrow \quad \frac{1}{\sin (\pi / n)}=\frac{1}{\sin (2 \pi / n)}+\frac{1}{\sin (3 \pi / n)} \\ & \Rightarrow \quad \frac{1}{\sin (\pi / n)}=\frac{\sin (\frac{3 \pi}{n})+\sin (\frac{2 \pi}{n})}{\sin (2 \pi / n) \sin (3 \pi / n)} \\ & \Rightarrow \quad \sin (\frac{2 \pi}{n}) \cdot \sin (\frac{3 \pi}{n})=\sin (\frac{\pi}{n}) \sin (\frac{3 \pi}{n}) \\ & +\sin (\frac{\pi}{n}) \cdot \sin (\frac{2 \pi}{n}) \\ & \Rightarrow \sin (\frac{2 \pi}{n}) [\sin (\frac{3 \pi}{n})-\sin (\frac{\pi}{n})]=\sin (\frac{\pi}{n}) \cdot \sin (\frac{3 \pi}{n}) \\ & \Rightarrow \sin (\frac{2 \pi}{n}) \quad [2 \cos (\frac{3 \pi+\pi}{2 n}) \sin (\frac{3 \pi-\pi}{2 n})] \\ & =\sin (\frac{\pi}{n}) \cdot \sin (\frac{3 \pi}{n}) \\ & \Rightarrow 2 \sin (\frac{2 \pi}{n}) \cdot \cos (\frac{2 \pi}{n}) \cdot \sin (\frac{\pi}{n})=\sin (\frac{\pi}{n}) \sin (\frac{3 \pi}{n}) \\ & \Rightarrow \quad 2 \sin (\frac{2 \pi}{n}) \cos (\frac{2 \pi}{n})=\sin (\frac{3 \pi}{n}) \\ & \Rightarrow \quad \sin (\frac{4 \pi}{n})=\sin (\frac{3 \pi}{n}) \\ & \Rightarrow \quad \frac{4 \pi}{n}=\pi-\frac{3 \pi}{n} \\ & \Rightarrow \quad \frac{7 \pi}{n}=\pi \\ & \Rightarrow \quad n=7 \end{aligned} $





