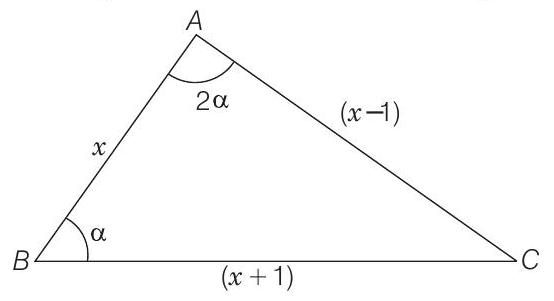
Properties Of Triangles Ques 13
The sides of a triangle are three consecutive natural numbers and its largest angle is twice the smallest one. Determine the sides of the triangle.
(1991, 4M)
Correct Answer: 13.($4, 5, 6$ units) Solution: Then, by sine rule, we have $\frac{\sin \alpha}{x-1} =\frac{\sin 2 \alpha}{x+1} $ $\Rightarrow \frac{\sin 2 \alpha}{\sin \alpha} =\frac{x+1}{x-1} $ $\Rightarrow 2 \cos \alpha =\frac{x+1}{x-1} $ $\therefore \cos \alpha =\frac{x+1}{2(x-1)}$ $\quad$ …….(i) Also, $\cos \alpha=\frac{x^{2}+(x+1)^{2}-(x-1)^{2}}{2 x(x+1)} \quad$ [using cosine law] $
\Rightarrow \quad \cos \alpha=\frac{x+4}{2(x+1)}
$ $\quad$ …….(ii) From Eqs. (i) and (ii), $
\begin{aligned}
& & \frac{x+1}{2(x-1)} & =\frac{x+4}{2(x+1)} \\
\Rightarrow & & (x+1)^{2} & =(x+4)(x-1) \\
\Rightarrow & & x^{2}+2 x+1 & =x^{2}+3 x-4 \\
\Rightarrow & & x & =5
\end{aligned}
$ Hence, the lengths of the sides of the triangle are $4$, $5$ and $6$ units.Show Answer
Answer: