Properties Of Triangles Ques 14
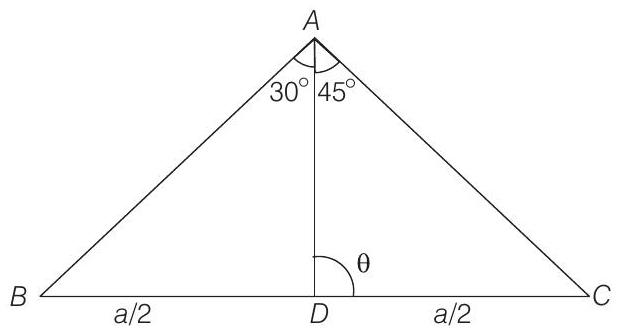
In a $\triangle A B C$, the median to the side $B C$ is of length $\frac{1}{\sqrt{11-6 \sqrt{3}}}$ and it divides the $\angle A$ into angles $30^{\circ}$ and $45^{\circ}$. Find the length of the side $B C$.
$(1985,5 M)$
Correct Answer: 14.$(2)$ Solution: $
\begin{aligned}
\Rightarrow \quad (\frac{a}{2}+\frac{a}{2}) \cot \theta & =\frac{a}{2} \cot 30^{\circ}-\frac{a}{2} \cot 45^{\circ} \\
\cot \theta & =\frac{\sqrt{3}-1}{2}
\end{aligned}
$ Applying sine rule in $\triangle A D C$, we get $
\frac{A D}{\sin \left(\pi-\theta-45^{\circ}\right)}=\frac{D C}{\sin 45^{\circ}}
$ $\Rightarrow \quad \frac{A D}{\sin \left(\theta+45^{\circ}\right)}=\frac{\frac{a}{2}}{\frac{1}{\sqrt{2}}} $ $\Rightarrow \quad A D=\frac{a}{\sqrt{2}}\left(\sin 45^{\circ} \cos \theta+\cos 45^{\circ} \sin \theta\right) $ $\Rightarrow \quad A D=\frac{a}{\sqrt{2}} \quad (\frac{\cos \theta+\sin \theta}{\sqrt{2}})=\frac{a}{2}(\cos \theta+\sin \theta) $ $\Rightarrow \quad \frac{1}{\sqrt{11-6 \sqrt{3}}}=\frac{a}{2} (\frac{\sqrt{3}-1}{\sqrt{8-2 \sqrt{3}}}+\frac{2}{\sqrt{8-2 \sqrt{3}}}) $ $\Rightarrow \quad a=\frac{2 \sqrt{8-2 \sqrt{3}}}{(\sqrt{3}+1) \sqrt{11-6 \sqrt{3}}}=\frac{2 \sqrt{8-2 \sqrt{3}}}{\sqrt{(\sqrt{3}+1)^{2}} \sqrt{11-6 \sqrt{3}}} $ $=\frac{2 \sqrt{8-2 \sqrt{3}}}{\sqrt{(4+2 \sqrt{3})(11-6 \sqrt{3})}} $ $=\frac{2 \sqrt{8-2 \sqrt{3}}}{\sqrt{44-24 \sqrt{3}+22 \sqrt{3}-36}} $ $=2 \frac{\sqrt{8-2 \sqrt{3}}}{\sqrt{8-2 \sqrt{3}}}=2$Show Answer
Answer: