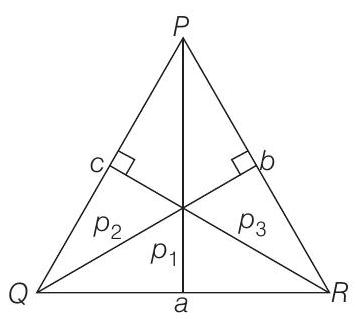
Properties Of Triangles Ques 2
If in a $\triangle P Q R, \sin P, \sin Q, \sin R$ are in $AP$, then
(a) the altitudes are in $AP$
(b) the altitudes are in $HP$
(c) the medians are in $GP$
(d) the medians are in $AP$
(1998, 2M)
Correct Answer: 2.(b) Solution: $
\frac{a}{\sin P}=\frac{b}{\sin Q}=\frac{c}{\sin R}=k
$ Also, $
\frac{1}{2} a p _1=\Delta
$ $
\begin{array}{ll}
\Rightarrow & \frac{2 \Delta}{a}=p _1 \\
\Rightarrow & p _1=\frac{2 \Delta}{k \sin P}
\end{array}
$ Similarly, $\quad p _2=\frac{2 \Delta}{k \sin Q}$ and $p _3=\frac{2 \Delta}{k \sin R}$ Since, $\sin P, \sin Q$ and $\sin R$ are in AP, hence $p _1, p _2, p _3$ are in HP.Show Answer
Answer:
Formula: