Properties Of Triangles Ques 22
If the angles of a triangle are in the ratio $4: 1: 1$, then the ratio of the longest side to the perimeter is
$(2003,1 M)$
(a) $\sqrt{3}:(2+\sqrt{3})$
(b) $1: 3: 2$
(c) $1: 2+\sqrt{3}$
(d) $2: 3$
Show Answer
Answer:
Correct Answer: 22.(a)
Solution:
- Given, ratio of angles are $4: 1: 1$.
$ \Rightarrow \quad 4 x+x+x=180^{\circ} $
$\Rightarrow \quad x =30^{\circ} $
$\therefore \quad \angle A=120^{\circ}, \angle B=\angle C =30^{\circ}$
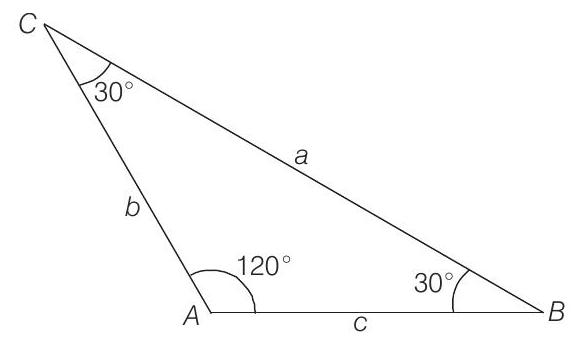
Thus, ratio of longest side to perimeter $=\frac{a}{a+b+c}$
$ \begin{aligned} & \text { Let } \quad b=c=x \\ & \Rightarrow \quad a^{2}=b^{2}+c^{2}-2 b c \cos A \quad \text { [by cosine rule] } \\ & \Rightarrow \quad a^{2}=2 x^{2}-2 x^{2} \cos A \\ & =2 x^{2}(1-\cos A) \\ & \Rightarrow \quad a^{2}=4 x^{2} \sin ^{2} A / 2 \\ & \Rightarrow \quad a=2 x \sin A / 2 \\ & \Rightarrow \quad a=2 x \sin 60^{\circ}=\sqrt{3} x \end{aligned} $
Thus, required ratio
$ \begin{aligned} & =\frac{a}{a+b+c} \\ & =\frac{\sqrt{3} x}{x+x+\sqrt{3} x} \\ & =\frac{\sqrt{3}}{2+\sqrt{3}} \\ & =\sqrt{3}: 2+\sqrt{3} \end{aligned} $





