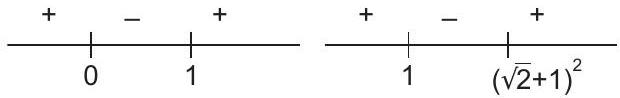Properties Of Triangles Ques 26
Let $A, B, C$ be three angles such that $A=\frac{\pi}{4}$ and $\tan B, \tan C=p$. Find all positive values of $p$ such that $A, B, C$ are the angles of triangle.
(1997C, 5M)
Correct Answer: 26.$(p \in(-\infty, 0) \cup 3+2 \sqrt{2}, \infty)$ Solution: $\Rightarrow \quad B+C=\pi-\pi / 4=3 \pi / 4$ $ \quad$ …….(i) $\therefore \quad 0<B, C<3 \pi / 4$ $[\because A=\pi / 4$, given $]$ Also, given $\quad \tan B \cdot \tan C=p$ $\Rightarrow \quad \frac{\sin B \cdot \sin C}{\cos B \cdot \cos C}=\frac{p}{1}$ $\Rightarrow \frac{\sin B \cdot \sin C+\cos B \cos C}{\sin B \cdot \sin C-\cos B \cdot \cos C}=\frac{p+1}{p-1}$ $\Rightarrow \quad \frac{\cos (B-C)}{\cos (B+C)}=\frac{1+p}{1-p}$ $
\Rightarrow \quad \cos (B-C)=-\frac{(1+p)}{\sqrt{2}(1-p)}
$$ \quad$ …….(ii) $
[\because B+C=3 \pi / 4]
$ Since, $B$ or $C$ can vary from 0 to $3 \pi / 4$ $\therefore 0 \leq B-C<3 \pi / 4 $ $\Rightarrow -\frac{1}{\sqrt{2}}<\cos (B-C) \leq 1$ $ \quad$ …….(iii) From Eqs. (ii) and (iii), $-\frac{1}{\sqrt{2}}<\frac{1+p}{\sqrt{2}(p-1)} \leq 1$ $
\begin{aligned}
& \Rightarrow \quad-\frac{1}{\sqrt{2}}<\frac{1+p}{\sqrt{2}(p-1)} \quad \text { and } \quad \frac{1+p}{\sqrt{2}(p-1)} \leq 1 \\
& \Rightarrow \frac{1+p}{p-1}+1 \geq 0 \text { and } \frac{1+p-\sqrt{2} p+\sqrt{2}}{\sqrt{2}(p-1)} \leq 0 \\
& \Rightarrow \quad \frac{2 p}{p-1} \geq 0 \text { and } \frac{(1-\sqrt{2}) p-\frac{1+\sqrt{2}}{1-\sqrt{2}}}{\sqrt{2}(p-1)} \leq 0 \\
& \Rightarrow \quad \frac{2 p}{p-1}>0 \quad \text { and } \quad \frac{\left(p-(\sqrt{2}+1)^{2}\right)}{(p-1)} \geq 0
\end{aligned}
$ $
\begin{aligned}
& \Rightarrow \quad(p<0 \text { or } p>1) \\
& \text { and } \quad\left(p<1 \text { or } p>(\sqrt{2}+1)^{2}\right)
\end{aligned}
$ On combining above expressions, we get $
\begin{array}{ll}
& p<0 \text { or } p \geq(\sqrt{2}+1)^{2} \\
\text { i.e. } & p \in(-\infty, 0) \cup\left[(\sqrt{2}+1)^{2}, \infty\right) \\
\text { or } & p \in(-\infty, 0) \cup[3+2 \sqrt{2}, \infty)
\end{array}
$Show Answer
Answer: