Properties Of Triangles Ques 3
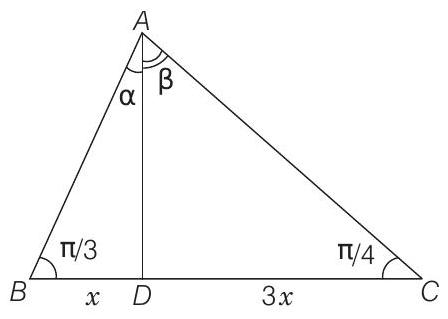
In a $\triangle A B C, \angle B=\frac{\pi}{3}$ and $\angle C=\frac{\pi}{4}$. Let $D$ divides $B C$ internally in the ratio $1: 3$, then $\frac{\sin \angle B A D}{\sin \angle C A D}$ is equal to
(a) $\frac{1}{\sqrt{6}}$
(b) $\frac{1}{3}$
(c) $\frac{1}{\sqrt{3}}$
(d) $\sqrt{\frac{2}{3}}$
(1995, 2M)
Show Answer
Answer:
Correct Answer: 3.(a)
Solution:
Formula:
- In $\triangle A B D$, applying sine rule, we get
$ \Rightarrow \quad \frac{A D}{\sin \pi / 3} =\frac{x}{\sin \alpha} $
$A D =\frac{\sqrt{3}}{2} x \sin \alpha \quad$ …….(i)
and in $\triangle A C D$, applying sine rule, we get
$\frac{A D}{\sin \pi / 4} =\frac{3 x}{\sin \beta} $
$A D =\frac{3}{\sqrt{2}} x \sin \beta \quad$ …….(ii)
From Eqs. (i) and (ii), $\frac{\sqrt{3} x}{2 \sin \alpha}=\frac{3 x}{\sqrt{2} \sin \beta}$
$ \Rightarrow \quad \frac{\sin \alpha}{\sin \beta}=\frac{1}{\sqrt{6}} $





