Properties Of Triangles Ques 33
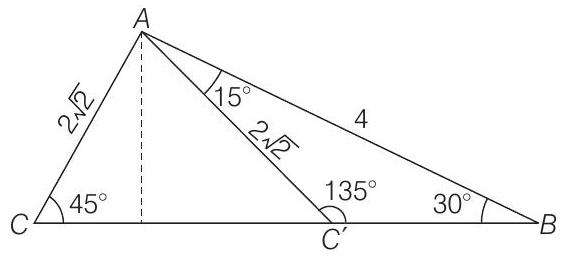
Let $A B C$ and $A B C^{\prime}$ be two non-congruent triangles with sides $A B=4, A C=A C^{\prime}=2 \sqrt{2}$ and angle $B=30^{\circ}$. The absolute value of the difference between the areas of these triangles is
(2009)
Correct Answer: 33.($4$ sq units) Solution: $
\Rightarrow \quad C=45^{\circ}, C^{\prime}=135^{\circ}
$ When, $C=45^{\circ} \Rightarrow A=180^{\circ}-\left(45^{\circ}+30^{\circ}\right)=105^{\circ}$ When, $C^{\prime}=135^{\circ} \Rightarrow A=180^{\circ}-\left(135^{\circ}+30^{\circ}\right)=15^{\circ}$ Area of $\triangle A B C=\frac{1}{2} A B \times A C \sin A$ $
=\frac{1}{2} \times 4 \times 2 \sqrt{2} \sin \left(105^{\circ}\right)
$ $
=4 \sqrt{2} \times \frac{\sqrt{3}+1}{2 \sqrt{2}}
$ $=2(\sqrt{3}+1)$ sq. units Area of $\triangle A B C^{\prime}=\frac{1}{2} A B \times A C \sin A$ $
\begin{aligned}
& =\frac{1}{2} \times 4 \times 2 \sqrt{2} \sin \left(15^{\circ}\right) \\
& =2(\sqrt{3}-1) \text { sq. units }
\end{aligned}
$ Difference of areas of triangle $
=|2(\sqrt{3}+1)-2(\sqrt{3}-1)|=4 \text { sq units }
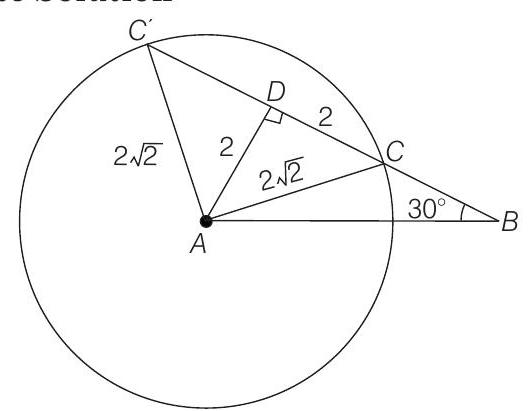
$ Alternate Solution Here, $A D=2, D C=2$ Difference of areas of $\triangle A B C$ and $\triangle A B C^{\prime}$ $=$ Area of $\triangle A C C^{\prime}$ $=\frac{1}{2} A D \times C C^{\prime}=\frac{1}{2} \times 2 \times 4=4 $ sq unitsShow Answer
Answer: