Properties Of Triangles Ques 34
If $P Q R$ is a triangle of area $\triangle$ with $a=2, b=\frac{7}{2}$ and $c=\frac{5}{2}$, where $a, b$ and $c$ are the lengths of the sides of the triangle opposite to the angles at $P, Q$ and $R$, respectively. Then, $\frac{2 \sin P-\sin 2 P}{2 \sin P+\sin 2 P}$ equals
(a) $\frac{3}{4 \Delta}$
(b) $\frac{45}{4 \Delta}$
(c) $(\frac{3}{4 \Delta})^2$
(d) $(\frac{45}{4 \Delta})^2$
(2012)
Show Answer
Answer:
Correct Answer: 34.(c)
Solution:
Formula:
Trigonometric Functions of Half Angles:
- PLAN: If $\triangle A B C$ has sides $a, b, c$.
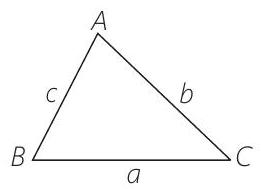
Then, $\quad \tan (A / 2)=\sqrt{\frac{(s-b)(s-a)}{s(s-a)}}$
$ \text { where, } \quad s=\frac{a+b+c}{2} $
$ \Rightarrow \quad s=\frac{2+\frac{7}{2}+\frac{5}{2}}{2}=4 $
$\therefore \frac{2 \sin P-\sin 2 P}{2 \sin P+\sin 2 P}=\frac{2 \sin P(1-\cos P)}{2 \sin P(1+\cos P)}$
$ =\frac{2 \sin ^{2}(P / 2)}{2 \cos ^{2}(P / 2)}=\tan ^{2}(P / 2) $
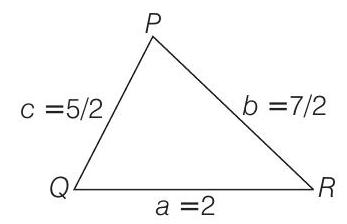
$ \begin{aligned} \Rightarrow \quad & \frac{(s-b)(s-c)}{s(s-a)} \times \frac{(s-b)(s-c)}{(s-b)(s-c)} \\ = & \frac{\left[(s-b)^{2}(s-c)^{2}\right]}{\Delta^{2}}=\frac{(4-\frac{7}{2})^{2} (4-\frac{5}{2})^{2}}{\Delta^{2}}=(\frac{3}{4 \Delta})^{2} \end{aligned} $





