Properties Of Triangles Ques 37
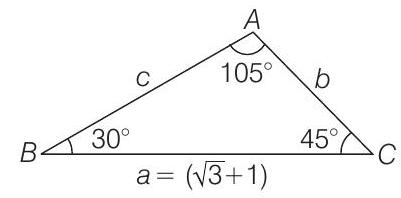
If the angle of a triangle are $30^{\circ}$ and $45^{\circ}$ and the included side is $(\sqrt{3}+1) cm$, then the area of the triangle is … .
(1988, 2M)
Show Answer
Answer:
Correct Answer: 37.($\frac{1+\sqrt{3}}{2}$ sq cm )
Solution:
Formula:
- By sine rule, $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$
$ \Rightarrow \quad \frac{\sqrt{3}+1}{\sin \left(105^{\circ}\right)}=\frac{b}{\sin 30^{\circ}} $
$ \Rightarrow \quad b=\frac{(\sqrt{3}+1) \sin 30^{\circ}}{\sin 105^{\circ}} $
$\therefore$ Area of triangle
$ =\frac{1}{2} a b \sin 45^{\circ}=\frac{1}{2}(\sqrt{3}+1) \frac{(\sqrt{3}+1) \sin 30^{\circ} \sin 45^{\circ}}{\sin 105^{\circ}} $
$ \begin{aligned} & =\frac{1}{2} \cdot \frac{(\sqrt{3}+1)^{2}}{\left(\sin 45^{\circ} \cos 60^{\circ}+\cos 45^{\circ} \sin 60^{\circ}\right)} \cdot \frac{1}{2} \cdot \frac{1}{\sqrt{2}} \\ & =\frac{1}{4 \sqrt{2}} \frac{(3+1+2 \sqrt{3})}{(\frac{1}{\sqrt{2}} \cdot \frac{1}{2}+\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{3}}{2})}=\frac{(4+2 \sqrt{3})}{4 \sqrt{2}(1+\sqrt{3})} \cdot 2 \sqrt{2} \\ & =\frac{(1+\sqrt{3})^{2}}{2(1+\sqrt{3})}=\frac{1+\sqrt{3}}{2} sq cm \end{aligned} $





