Properties Of Triangles Ques 5
Let $A B C$ be a triangle such that $\angle A C B=\frac{\pi}{6}$. If $a, b$ and $c$ denote the lengths of the sides opposite to $A, B$ and $C$ respectively. Then, the value(s) of $x$ for which $a=x^{2}+x+1, b=x^{2}-1$ and $c=2 x+1$ is (are) (2010)
(a) $-(2+\sqrt{3})$
(b) $1+\sqrt{3}$
(c) $2+\sqrt{3}$
(d) $4 \sqrt{3}$
Show Answer
Answer:
Correct Answer: 5.(b)
Solution:
- Using, $\cos C=\frac{a^{2}+b^{2}-c^{2}}{2 a b}$
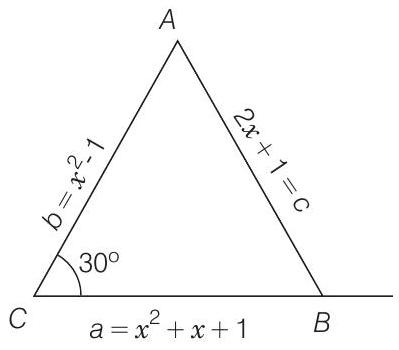
$\Rightarrow \quad \frac{\sqrt{3}}{2}=\frac{\left(x^{2}+x+1\right)^{2}+\left(x^{2}-1\right)^{2}-(2 x+1)^{2}}{2\left(x^{2}+x+1\right)\left(x^{2}-1\right)}$
$\Rightarrow \quad(x+2)(x+1)(x-1) x+\left(x^{2}-1\right)^{2}=\sqrt{3}\left(x^{2}+x+1\right)\left(x^{2}-1\right)$
$\Rightarrow \quad x^{2}+2 x+\left(x^{2}-1\right)=\sqrt{3}\left(x^{2}+x+1\right)$
$\Rightarrow \quad(2-\sqrt{3}) x^{2}+(2-\sqrt{3}) x-(\sqrt{3}+1)=0$
$\Rightarrow \quad x =-(2+\sqrt{3}) $
and $ \quad x =1+\sqrt{3} $
But $ \quad x =-(2+\sqrt{3})$
$\Rightarrow \quad c$ is negative.
$\therefore x=1+\sqrt{3}$ is the only solution.





