Properties Of Triangles Ques 57
In a $\triangle A B C$, let $\angle C=\pi / 2$. If $r$ is the inradius and $R$ is the circumradius of the triangle, then $2(r+R)$ is equal to
$(2000,2 M)$
(a) $a+b$
(b) $b+c$
(c) $c+a$
(d) $a+b+c$
Show Answer
Answer:
Correct Answer: 57.(a)
Solution:
Formula:
- Here, $R^{2}=M C^{2}=\frac{1}{4}\left(a^{2}+b^{2}\right) \quad$ [by distance from origin]
$=\frac{1}{4} c^{2} \quad$ [by Pythagoras theorem]
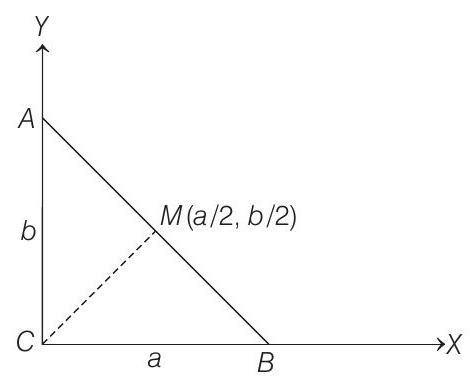
$ \Rightarrow \quad R=\frac{c}{2} $
Next, $\quad r=(s-c) \tan (C / 2)=(s-c) \tan \pi / 4=s-c$
$\therefore \quad 2(r+R)=2 r+2 R=2 s-2 c+c$
$ \begin{aligned} & =a+b+c-c \\ & =a+b \end{aligned} $
BETA
