Sequences And Series Ques 82
If $(10)^{9}+2(11)^{1}(10)^{8}+3(11)^{2}(10)^{7}+\ldots+10(11)^{9}=k(10)^{9}$, then $k$ is equal to
(2014 Main)
(a) $\frac{121}{10}$
(b) $\frac{441}{100}$
(c) $100$
(d) $110$
Show Answer
Answer:
Correct Answer: 82.(c)
Solution:
Formula:
Arithmetico-Geometrical Progression (A.G.P.):
- Given,
$ \begin{aligned} & k \cdot 10^{9}=10^{9}+2(11)^{1}(10)^{8}+3(11)^{2}(10)^{7}+\ldots+10(11)^{9} \\ & \Rightarrow \quad k=1+2 (\frac{11}{10})+3 (\frac{11}{10})^{2}+\ldots+10 (\frac{11}{10}) \quad …….(i) \\ & \frac{11}{10} k=1 \quad (\frac{11}{10})+2 (\frac{11}{10})^{2}+\ldots+9 (\frac{11}{10})^{9}+10 (\frac{11}{10}) \ldots \quad …….(ii) \end{aligned} $
On subtracting Eq. (ii) from Eq. (i), we get
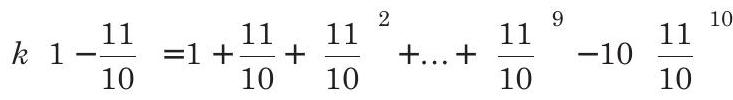
$ \begin{aligned} & \Rightarrow k (\frac{10-11}{10})=\frac{1 [(\frac{11}{10})^{10}-1]}{(\frac{11}{10}-1)}-10 (\frac{11}{10})^{10} \end{aligned} $
$[\because$ In GP, sum of $n$ terms $=\frac{a\left(r^{n}-1\right)}{r-1}$, when $r>1]$
$ \begin{array}{ll} \Rightarrow & -k=10[10 (\frac{11}{10})^{10}-10-10 (\frac{11}{10})^{10} ]\\ \therefore & k=100 \end{array} $





