Electromagnetic Induction And Alternating Current Ques 93
93. The change in the magnetic dipole moment associated with the orbit, at the end of the time interval of the magnetic field change, is
(a) $\gamma B Q R^{2}$
(b) $-\mathrm{v} \frac{B Q R^{2}}{2}$
(c) $\gamma \frac{B Q R^{2}}{2}$
(d) $\gamma B Q R^{2}$
Show Answer
Answer:
Correct Answer: 93.(b)
Solution:
- $\frac{M}{L}=\frac{Q}{2 m}$
$\therefore \quad M=\frac{Q}{2 m} L \quad \Rightarrow \quad M \propto L$, where $\gamma=\frac{Q}{2 m}$
$$ =\frac{Q}{2 m} \quad(I \omega)=\frac{Q}{2 m} \quad\left(m R^{2} \omega\right)=\frac{Q \omega R^{2}}{2} $$
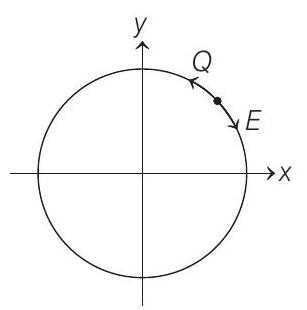
Induced electric field is in the opposite direction. Therefore,
$$ \begin{aligned} \omega^{\prime} & =\omega-\alpha t \\ \alpha & =\frac{\tau}{I}=\frac{(Q E) R}{m R^{2}} \\ & =\frac{(Q) \frac{B R}{2} R}{m R^{2}}=\frac{Q B}{2 m} \\ \therefore \quad \omega^{\prime} & =\omega-\frac{Q B}{2 m} \cdot 1=\omega-\frac{Q B}{2 m} \\ M_{f} & =\frac{Q \omega^{\prime} R^{2}}{2}=Q \omega-\frac{Q B}{2 m} \frac{R^{2}}{2} \end{aligned} $$
$$ \begin{array}{rlr} \therefore \Delta M & =M_{f}-M_{i}=-\frac{Q^{2} B R^{2}}{4 m} & \\ M & =-\gamma \frac{Q B R^{2}}{2} & (\because \gamma=\frac{Q}{2 m}) \end{array} $$





