Electrostatics Ques 181
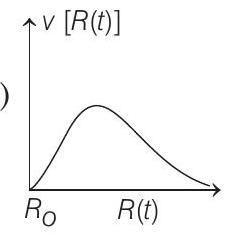
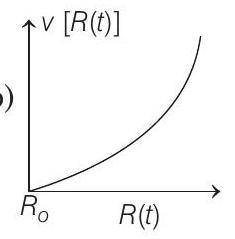
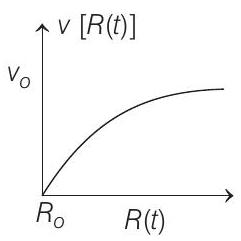
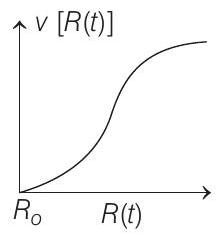
- There is uniform spherically symmetric surface charge density at a distance $R_{0}$ from the origin. The charge distribution is initially at rest and starts expanding because of mutual repulsion. The figure that represents best the speed $v[R(t)]$ of the distribution as a function of its instantaneous radius $R(t)$ is
(Main 2019, 12 Jan I)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 181.(c)
Solution:
Formula:
Electrostatic Potential Energy
- Key Idea As, electrostatic force is conserved in nature so, total energy of charge distribution remains constant in absence of any external interaction.
Let radius of distribution at some instant $t$ is $R$. At $t=0$, radius is given $R_{0}$
Now by conservation of energy, we have
$$ 0+\frac{k Q^{2}}{2 R_{0}}=\frac{1}{2} m v^{2}+\frac{k Q^{2}}{2 R} $$
( $\because$ The distribution starts from rest, so, initial kinetic energy is zero.)
Differentiating this equation with respect to $R$, we get
$$ \frac{1}{2} m 2 v \frac{d v}{d R}-\frac{k Q^{2}}{2 R^{2}}=0 \text { or } \frac{d v}{d R}=\frac{k Q^{2}}{2 m v R^{2}} $$
Here, $\frac{d v}{d R}=$ slope of $v$ versus $R$ graph. It decreases with increasing $v$ and $R$.
Also, slope $\quad \longrightarrow 0$ as $R \quad \longrightarrow \infty$.
From above conclusions, we can see that the best suited graph is given in option (c).





