Magnetics Ques 108
- A moving coil galvanometer, having a resistance $G$, produces full scale deflection when a current $I _g$ flows through it. This galvanometer can be converted into (i) an ammeter of range 0 to $I _0\left(I _0>I _g\right)$ by connecting a shunt resistance $R _A$ to it and (ii) into a voltmeter of range 0 to $V\left(V=G I _0\right)$ by connecting a series resistance $R _V$ to it. Then,
(2019 Main, 12 April II)
(a) $R _A R _V=G^{2} (\frac{I _0-I _g}{I _g})$ and $\frac{R _A}{R _V}=(\frac{I _g}{\left(I _0-I _g\right)})^2$
(b) $R _A R _V=G^{2}$ and $\frac{R _A}{R _V}=(\frac{I _g}{I _0-I _g})^2$
(c)
(d)
Show Answer
Answer:
Correct Answer: 108.(b)
Solution:
Formula:
- To use galvanometer as an ammeter, a low resistance in parallel is used.
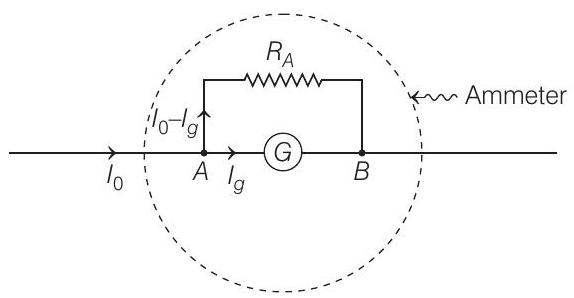
In ammeter, if $I _g=$ full scale deflection current, then equating potential drops across points marked $A B$, we have
$ V _{A B}=I _g G=\left(I _0-I _g\right) R _A $
$ \Rightarrow \quad R _A=\frac{I _g G}{I _0-I _g} $ $\quad$ …….(i)
Here, $G$ =resistance of galvanometer coil.
When a galvanometer is used as a voltmeter, a high resistance $\left(R _V\right)$ in series is used.
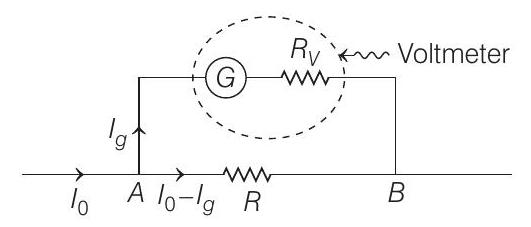
Equating potential across point $A B$,
$V _{A B}=\left(G+R _V\right) I _g $
$\text { But } V _{A B}=I _0 G \quad $ (given)
$\text { So, } I _0 G=\left(G+R _V\right) I _g $
$\Rightarrow R _V=\frac{\left(I _0-I _g\right) G}{I _g}$ $\quad$ …….(ii)
From Eqs. (i) and (ii), we have
$ \frac{R _A}{R _V}=\frac{(\frac{I _g G}{I _0-I _g})}{\frac{\left(I _0-I _g\right) G}{I _g}}=\frac{I _g^{2}}{\left(I _0-I _g\right)^{2}} $
and $\quad R _A \times R _V=\frac{I _g G}{\left(I _0-I _g\right)} \times \frac{\left(I _0-I _g\right) G}{I _g}=G^{2}$





