Magnetics Ques 117
- In the $x y$-plane, the region $y>0$ has a uniform magnetic field $B _1 \hat{k}$ and the region $y<0$ has another uniform magnetic field $B _2 \hat{k}$. A positively charged particle is projected from the origin along the positive $Y$-axis with speed $v _0=\pi ms^{-1}$ at $t=0$, as shown in figure. Neglect gravity in this problem. Let $t=T$ be the time when the particle crosses the $X$-axis from below for the first time. If $B _2=4 B _1$, the average speed of the particle, in $ms^{-1}$, along the $X$-axis in the time interval $T$ is…….
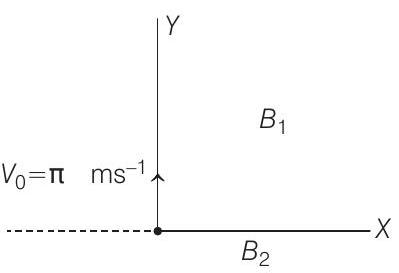(2018 Adv.)
Show Answer
Answer:
Correct Answer: 117.$(2)$
Solution:
Formula:
Magnetic Force Acting On A Moving Point Charge:
- If average speed is considered along $x$-axis,
$ \begin{gathered} R _1=\frac{m v _0}{q B _1}, R _2=\frac{m v _0}{q B _2}=\frac{m v _0}{4 q B _1} \\ R _1>R _2 \end{gathered} $
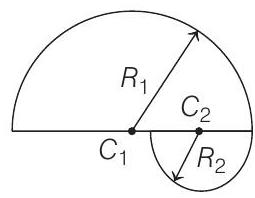
Distance travelled along $x$-axis, $\Delta x=2\left(R _1+R _2\right)=\frac{5 m v _0}{2 q B _1}$
Total time $=\frac{T _1}{2}+\frac{T _2}{2}=\frac{\pi m}{q B _1}+\frac{\pi m}{q B _2}$
$ =\frac{\pi m}{q B _1}+\frac{\pi m}{4 q B _1}=\frac{5 \pi m}{4 q B _1} $
Magnitude of average speed $=\frac{\frac{5 m v _0}{2 q B _1}}{\frac{5 \pi m}{4 q B _1}}=2$
BETA
