Magnetics Ques 23
- A particle of charge $+q$ and mass $m$ moving under the influence of a uniform electric field $E \hat{\mathbf{i}}$ and uniform magnetic field $B \hat{\mathbf{k}}$ follows a trajectory from $P$ to $Q$ as shown in figure. The velocities at $P$ and $Q$ are $v \hat{\mathbf{i}}$ and $-2 \hat{\mathbf{j}}$. Which of the following statement(s) is/are correct?
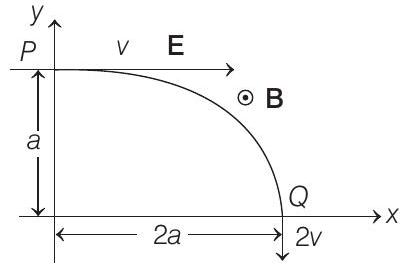
$(1991,2 M)$
(a) $E=\frac{3}{4} [\frac{m v^{2}}{q a}]$
(b) Rate of work done by the electric field at $P$ is $\frac{3}{4} [\frac{m v^{3}}{a}]$
(c) Rate of work done by the electric field at $P$ is zero
(d) Rate of work done by both the fields at $Q$ is zero
Show Answer
Answer:
Correct Answer: 23.(a, b, d)
Solution:
Formula:
Magnetic Force Acting On A Moving Point Charge:
- Magnetic force does not do work. From work-energy theorem :
$ \begin{gathered} W _{F _e}=\Delta KE \text { or }(q E)(2 a)=\frac{1}{2} m\left[4 v^{2}-v^{2}\right] \\ \text { or } \quad E=\frac{3}{4} (\frac{m v^{2}}{q a}) \end{gathered} $
At $P$, rate of work done by electric field
$ \begin{aligned} & =\mathbf{F} _e \cdot \mathbf{v}=(q E)(v) \cos 0^{\circ} \\ & =q (\frac{3}{4} \frac{m v^{2}}{q a}) v=\frac{3}{4} (\frac{m v^{3}}{a}) \end{aligned} $
Therefore, option (b) is also correct.
Rate of work done at $Q$ :
of electric field $=\mathbf{F} _e \cdot \mathbf{v}=(q E)(2 v) \cos 90^{\circ}=0$
and of magnetic field is always zero. Therefore, option (d)
is also correct.
Note that $\mathbf{F} _e=q E \hat{\mathbf{i}}$.





