Magnetics Ques 35
- An electron gun $G$ emits electrons of energy $2$ $keV$ travelling in the positive $x$-direction. The electrons are required to hit the spot $S$ where $G S=0.1$ $ m$, and the line $G S$ make an angle of $60^{\circ}$ with the $x$-axis as shown in figure. A uniform magnetic field B parallel to $G S$ exists in the region outside the electron gun.
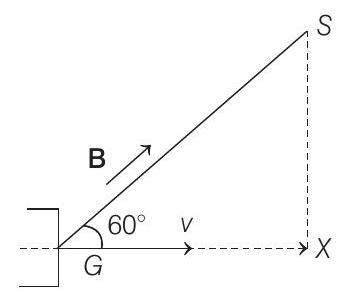
Find the minimum value of $B$ needed to make the electrons hit $S$.
(1993, 7M)
Show Answer
Answer:
Correct Answer: 35.$(4.73 \times 10^{-3} T)$
(b) $\mathbf{v} _f=-v _0 \hat{\mathbf{i}}, t=\frac{\pi m}{B _0 q}$
Solution:
Formula:
Magnetic Force Acting On A Moving Point Charge:
- Kinetic energy of electron, $K=\frac{1}{2} m v^{2}=2 keV$
$\therefore$ Speed of electron, $v=\sqrt{\frac{2 K}{m}}$
$ v=\sqrt{\frac{2 \times 2 \times 1.6 \times 10^{-16}}{9.1 \times 10^{-31}}} m / s=2.65 \times 10^{7} m / s $
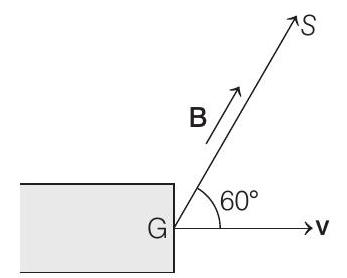
Since, the velocity $(\mathbf{v})$ of the electron makes an angle of $\theta=60^{\circ}$ with the magnetic field $\mathbf{B}$, the path will be a helix. So, the particle will hit $S$ if GS $=np$
Here, $n=1,2,3$
$ p=\text { pitch of helix }=\frac{2 \pi m}{q B} v \cos \theta $
But for $B$ to be minimum, $n=1$
Hence, $\quad G S=p=\frac{2 \pi m}{q B} v \cos \theta$
$ B=B _{\min }=\frac{2 \pi m v \cos \theta}{q(G S)} $
Substituting the values, we have
$ \begin{aligned} B _{\text {min }} & =\frac{(2 \pi)\left(9.1 \times 10^{-31}\right)\left(2.65 \times 10^{7}\right) (\frac{1}{2})}{\left(1.6 \times 10^{-19}\right)(0.1)} \\ B _{\text {min }} & =4.73 \times 10^{-3} T \end{aligned} $





