Magnetics Ques 47
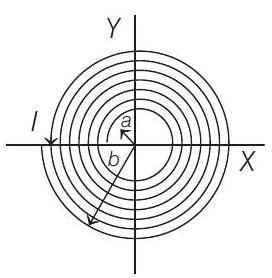
- A long insulated copper wire is closely wound as a spiral of $N$ turns. The spiral has inner radius $a$ and outer radius $b$. The spiral lies in the $X-Y$ plane and a steady current $I$ flows through the wire. The $Z$-component of the magnetic field at the centre of the spiral is
(2011)
(a) $\frac{\mu _0 N I}{2(b-a)} \ln (\frac{b}{a})$
(b) $\frac{\mu _0 N I}{2(b-a)} \ln (\frac{b+a}{b-a})$
(c) $\frac{\mu _0 N I}{2 b} \ln (\frac{b}{a})$
(d) $\frac{\mu _0 N I}{2 b} \ln (\frac{b+a}{b-a})$
Show Answer
Answer:
Correct Answer: 47.(a)
Solution:
Formula:
Magnetic Field Due To Infinite Straight Wire:
- If we take a small strip of $d r$ at distance $r$ from centre, then number of turns in this strip would be,
$ d N=(\frac{N}{b-a}) d r $
Magnetic field due to this element at the centre of the coil will be
$ \begin{aligned} \quad d B & =\frac{\mu _0(d N) I}{2 r}=\frac{\mu _0 N I}{(b-a)} \frac{d r}{r} \\ \therefore \quad B & =\int _{r=a}^{r=b} d B=\frac{\mu _0 N I}{2(b-a)} \ln \left(\frac{b}{a}\right) \end{aligned} $





