Magnetics Ques 70
- A long horizontal wire $A B$, which is free to move in a vertical plane and carries a steady current of $20 A$, is in equilibrium at a height of $0.01$ $m$ over another parallel long wire $C D$ which is fixed in a horizontal plane and carries a steady current of $30$ $A$, as shown in figure. Show that when $A B$ is slightly depressed, it executes simple harmonic motion. Find the period of oscillations.
$(1994,6$ M)
$ A \leftarrow B$
$ C \longrightarrow D $
Show Answer
Answer:
Correct Answer: 70.$(0.2$ $s)$
Solution:
Formula:
Magnetic Moment Of A Current Carrying Loop:
- Let $m$ be the mass per unit length of wire $A B$. At a height $x$ above the wire $C D$, magnetic force per unit length on wire $A B$ will be given by
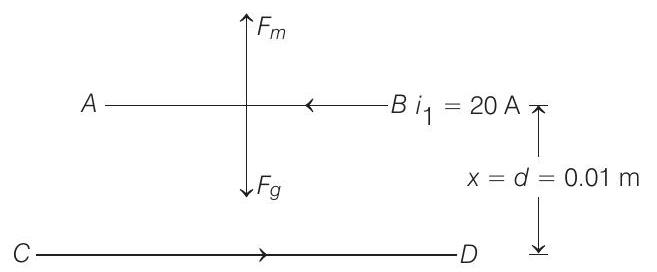
$ F _m=\frac{\mu _0}{2 \pi} \frac{i _1 i _2}{x} \quad \text { (upwards) } \quad …….(i) $
Weight per unit length of wire $A B$ is
$ F _g=m g \quad $ (downwards)
Here, $m=$ mass per unit length of wire $A B$
At $\quad x=d$, wire is in equilibrium i.e.,
$F _m =F _g $
$\text { or } \quad \frac{\mu _0}{2 \pi} \frac{i _1 i _2}{d} =m g $
$\text { or } \quad \frac{\mu _0}{2 \pi} \frac{i _1 i _2}{d^{2}} =\frac{m g}{d} \quad …….(ii)$
When $A B$ is depressed, $x$ decreases therefore, $F _m$ will increase, while $F _g$ remains the same. Let $A B$ is displaced by $d x$ downwards.
Differentiating Eq. (i) w.r.t. $x$, we get
$ d F _m=-\frac{\mu _0}{2 \pi} \frac{i _1 i _2}{x^{2}} \cdot d x \quad …….(iii) $
i.e. restoring force, $F=d F _m \propto-d x$
Hence, the motion of wire is simple harmonic.
From Eqs. (ii) and (iii), we can write
$ d F _m=-(\frac{m g}{d}) \cdot d x \quad(\because x=d) $
$\therefore$ Acceleration of wire $a=-(\frac{g}{d}) \cdot d x$
Hence, period of oscillation
$ \begin{aligned} T & =2 \pi \sqrt{\left|\frac{d x}{a}\right|} \\ & =2 \pi \sqrt{\frac{\mid \text { displacement } \mid}{\mid \text { acceleration } \mid}} \\ T & =2 \pi \sqrt{\frac{d}{g}} \\ & =2 \pi \sqrt{\frac{0.01}{9.8}} \\ T & =0.2 s \end{aligned} $





