Magnetics Ques 81
- Two magnetic dipoles $X$ and $Y$ are placed at a separation $d$, with their axes perpendicular to each other. The dipole moment of $Y$ is twice that of $X$. A particle of charge $q$ is passing $(2 M)$ through their mid-point $P$, at angle $\theta=45^{\circ}$ with the horizontal line, as shown in figure. What would be the magnitude of force on the particle at that instant? ( $d$ is much larger than the dimensions of the dipole)
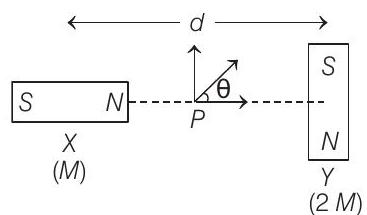
(2019 Main, 8 April II)
(a) $(\frac{\mu _0}{4 \pi}) \frac{M}{(\frac{d}{2})^{3}} \times q v$
(b) 0
(c) $\sqrt{2} (\frac{\mu _0}{4 \pi}) \frac{M}{(\frac{d}{2})^{3}} \times q v$
(d) $(\frac{\mu _0}{4 \pi}) \frac{2 M}{(\frac{d}{2})^{3}} \times q v$
Show Answer
Answer:
Correct Answer: 81.(b)
Solution:
Formula:
Magnetic Moment Of A Current Carrying Loop:
- Let $2 l _1$ and $2 l _2$ be the length of dipole $X$ and $Y$, respectively. For dipole $X$, point $P$ lies on its axial line. So, magnetic field strength at $P$ due to $X$ is
$ \mathbf{B} _X=\frac{\mu _0}{4 \pi} \cdot \frac{2 M r}{\left(r^{2}-l _1^{2}\right)^{2}}, \text { along } O P $
Here,
$ r=\frac{d}{2} $
Also,
$ d \gg l _1 $
$\Rightarrow\left|\mathbf{B} _X\right|=\frac{\mu _0}{4 \pi} \cdot \frac{2 M(d / 2)}{(d / 2)^{4}}=\frac{\mu _0}{4 \pi} \frac{2 M}{(d / 2)^{3}}$
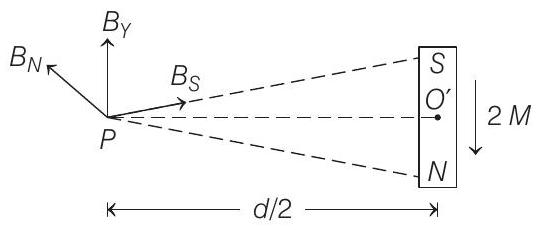
Similarly, for dipole $Y$, point $P$ lies on its equatorial line. So, magnetic field strength at $P$ due to $Y$ is
$\mathbf{B} _Y=\frac{\mu _0}{4 \pi} \cdot \frac{2 M}{\left(r^{2}+l _2^{2}\right)^{3 / 2}},\left(\right.$ along a line perpendicular to $\left.O^{\prime} P\right)$
Here,
$ r=\frac{d}{2} $
Also,
$ d \gg l _2 $
$\Rightarrow$ $ \left|\mathbf{B} _Y\right|=\frac{\mu _0}{4 \pi} \frac{2 M}{(d / 2)^{3}} $
Thus, the resultant magnetic field due to $X$ and $Y$ at $P$ is
Since,
$ \mathbf{B} _{\text {net }}=\mathbf{B} _X+\mathbf{B} _Y $
$ \left|\mathbf{B} _Y\right|=\left|\mathbf{B} _X\right| $
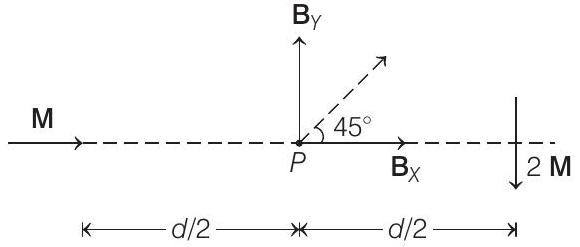
Thus, the resultant magnetic field $\left(\mathbf{B} _{\text {net }}\right.$ ) at $P$ will be at $45^{\circ}$ with the horizontal.
This means, direction of $\mathbf{B} _{\text {net }}$ and velocity of the charged particle is same.
$\therefore$ Force on the charged particle moving with velocity $v$ in the presence of magnetic field which is
$ \mathbf{B}=q(\mathbf{v} \times \mathbf{B})=q|\mathbf{v} | \mathbf{B}| \sin \theta $
where, $\theta$ is the angle between $\mathbf{B}$ and $\mathbf{v}$
According to the above analysis, we get
$ \begin{aligned} \therefore & & \theta & =0 \\ \therefore & & \mathbf{F} & =0 \end{aligned} $
Thus, magnitude of force on the particle at that instant is zero.





