Magnetics Ques 94
- A loop carrying current $I$ lies in the $x-y$ plane as shown in the figure. The unit vector $\hat{\mathbf{k}}$ is coming out of the plane of the paper. The magnetic moment of the current loop is
(2012)
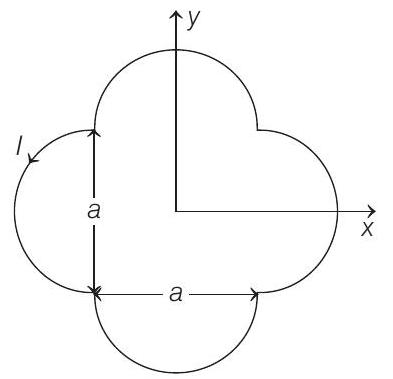
(a) $a^{2} I \hat{\mathbf{k}}$
(b) $(\frac{\pi}{2}+1) a^{2} I \hat{\mathbf{k}}$
(c) $-(\frac{\pi}{2}+1) a^{2} I \hat{\mathbf{k}}$
(d) $(2 \pi+1) a^{2} I \hat{\mathbf{k}}$
Show Answer
Answer:
Correct Answer: 94.(b)
Solution:
Formula:
Magnetic Moment Of A Current Carrying Loop:
- Area of the given loop is not provided
$A=$ (area of two circles of radius $\frac{a}{2}$ and area of a square of side $a$ )
$ \begin{aligned} &=2 \pi (\frac{a}{2}^{2}+a^{2})^{2}=(\frac{\pi}{2}+1) a^{4} \ |\mathbf{M}|=I A=(\frac{\pi}{4}+1) a^{2} I \end{aligned} $
From screw rule direction of $\mathbf{M}$ is outwards or in positive $z$-direction.
$ \therefore \quad \mathbf{M}=(\frac{\pi}{2}+1) a^{2} I \hat{\mathbf{k}} $





