Modern Physics Ques 166
- A proton is fired from very far away towards a nucleus with charge $Q=120$ $ e$, where $e$ is the electronic charge. It makes a closest approach of $10$ $ fm$ to the nucleus. The de-Broglie wavelength (in units of $fm$ ) of the proton at its start is [Take the proton mass, $m _p=(5 / 3) \times 10^{-27} $ $kg ; h / e=4.2 \times 10^{-15}$ $J-s / C$; $\frac{1}{4 \pi \varepsilon _0}=9 \times 10^{9}$ $ m / F ; 1 fm=10^{-15} m]$
(2013 Adv.)
Show Answer
Answer:
Correct Answer: 166.$(7)$
Solution:
Formula:
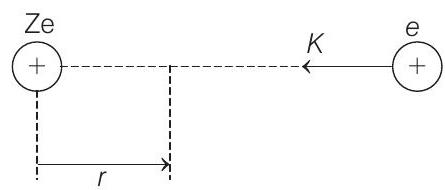
$r=$ closest distance $=10 $ $fm$.
From energy conservation, we have
$K _i+U _i =K _f+U _f $
$\text { or } =0+\frac{1}{4 \pi \varepsilon _0} \cdot \frac{q _1 q _2}{r} $
$K =\frac{1}{4 \pi \varepsilon _0} \cdot \frac{(120 e)(e)}{r} $ $\quad$ …….(i)
de-Broglie wavelength
$ \lambda=\frac{h}{\sqrt{2 K m}} $ $\quad$ …….(ii)
Substituting the given values in above two equations, we get
$ \lambda=7 \times 10^{-15} m=7$ $ fm $





