Modern Physics Ques 249
- The figure represents a voltage regulator circuit using a Zener diode. The breakdown voltage of the Zener diode is $6 $ $V$ and the load resistance is $R _L=4$ $ k \Omega$. The series resistance of the circuit is $R _i=1$ $ k \Omega$. If the battery voltage $V _B$ varies from $8$ $ V$ to $16 $ $V$, what are the minimum and maximum values of the current through Zener diode?
(Main 2019, 10 April II)

(a) $1.5 $ $mA, 8.5 $ $mA$
(b) $1 $ $mA, 8.5 $ $mA$
(c) $0.5 $ $mA, 8.5 $ $mA$
(d) $0.5 $ $mA, 6 $ $mA$
Show Answer
Answer:
Correct Answer: 249.(c)
Solution:
- In given voltage regulator circuit,

Zener breakdown voltage, $V _Z=6 $ $V$
So, across $R _L$, potential drop is always $6 $ $V$.
So, current through load resistance is
$ i _L=\frac{V _Z}{R _L}=\frac{6}{4 \times 10^{3}}=1.5 \times 10^{-3} A $
Now, when $V _B=8$ $ V$
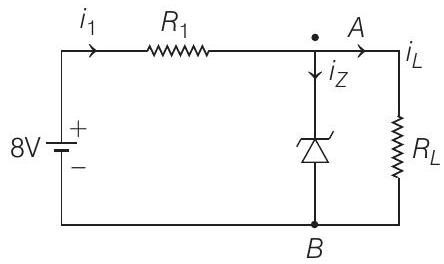
Potential drop across $R _1=8-6=2 $ $V$
So, current through $R _1$ is $i _1=\frac{V}{R _1}=\frac{2}{1 \times 10^{3}}=2 \times 10^{-3} $ $A$
So, current through Zener diode is
$ \begin{aligned} i _Z & =i _1-i _L=2 \times 10^{-3}-1.5 \times 10^{-3} \\ & =0.5 \times 10^{-3} A=0.5 mA \end{aligned} $
Similarly, when $V _B=16 $ $V$
$ \begin{array}{rlrl} & V _{R _1} =16-6=10 V \\ \therefore & i _1 =\frac{10}{1 \times 10^{3}}=10 \times 10^{-3} A \end{array} $
Hence,
$ \begin{aligned} i _Z & =i _1-i _L=10 \times 10^{-3}-1.5 \times 10^{-3} \\ & =8.5 \times 10^{-3} A=8.5 mA \end{aligned} $





