Modern Physics Ques 259
- A nucleus $A$, with a finite de-Broglie wavelength $\lambda _A$, undergoes spontaneous fission into two nuclei $B$ and $C$ of equal mass. $B$ flies in the same directions as that of $A$, while $C$ flies in the opposite direction with a velocity equal to half of that of $B$. The de-Broglie wavelengths $\lambda _B$ and $\lambda _C$ of $B$ and $C$ respectively
(Main 2019, 8 April II)
(a) $2 \lambda _A, \lambda _A$
(b) $\frac{\lambda _A}{2}, \lambda _A$
(c) $\lambda _A, 2 \lambda _A$
(d) $\lambda _A, \frac{\lambda _A}{2}$
Show Answer
Answer:
Correct Answer: 259.(b)
Solution:
Formula:
- Let $m$ be the mass of nuclei $B$ and $C$.
So, the given situation can be shown in the figure below
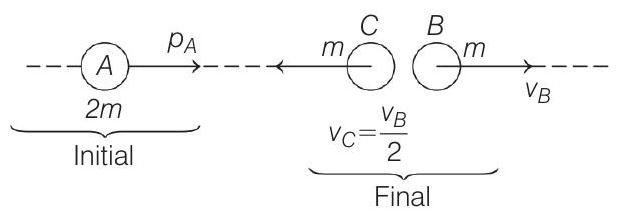
Now, according to the conservation of linear momentum, Initial momentum $=$ Final momentum
$ \begin{aligned} \Rightarrow \quad p _A & =p _B+p _C \text { or } 2 m v _A=m v _B+m v _C \\ 2 m v _A & =m v _B-\frac{m v _B}{2} \\ \Rightarrow \quad 2 v _A & =\frac{1}{2} v _B \quad \Rightarrow \quad v _B=4 v _A \quad …….(i) \\ \text { and } \quad v _C & =\frac{v _B}{2}=2 v _A \quad …….(ii) \end{aligned} $
So, momentum of $B$ and $C$ respectively, can now be given as
$ p _B=m _B v _B=m 4 v _A=2\left(2 m v _A\right) $
or $ \quad p _B=2 p _A \quad …….(iii)$
and $\quad p _C=m _C v _C=m 2 v _A \quad$ [using Eq. (ii)]
or $\quad p _C=p _A \quad …….(iv)$
From the relation of de-Broglie wavelength, i.e. $\lambda=\frac{h}{p}$
where, $p$ is momentum and $h$ is Planck’s constant.
So, for $A, \lambda _A=\frac{h}{p _A}$ or $p _A=\frac{h}{\lambda _A} \quad …….(v)$
From Eq. (v), $\lambda _B$ can be written as
$ \lambda _B=\frac{h}{2 \times \frac{h}{\lambda _A}}=\frac{\lambda _A}{2} $
Similarly, for $C, \lambda _C=\frac{h}{p _C}=\frac{h}{p _A} \quad $ [using Eq. (iv)]
Similarly, from Eq. (v), $\lambda _C$ can be written as
$ \lambda _C=\frac{h}{\frac{h}{\lambda _A}}=\lambda _A $





