Modern Physics Ques 293
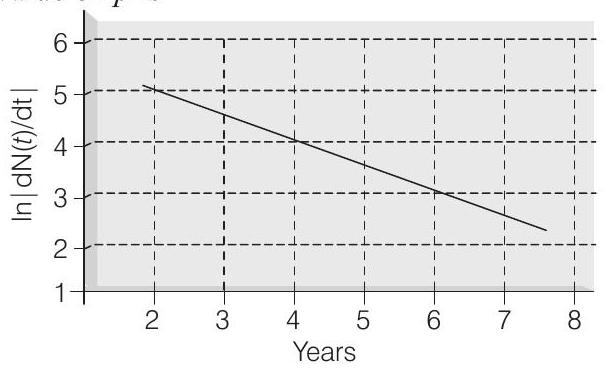
- To determine the half-life of a radioactive element, a student plots a graph of $\ln |\frac{d N(t)}{d t}|$ versus $t$. Here $\frac{d N(t)}{d t}$ is the rate of radioactive decay at time $t$. If the number of radioactive nuclei of this element decreases by a factor of $p$ after $4.16$ $ yr$, the value of $p$ is
(2010)
Show Answer
Answer:
Correct Answer: 293.$(8 )$
Solution:
Formula:
- $|\frac{d N}{d t}|=\mid$ Activity of radioactive substance $\mid$
$ =\lambda N=\lambda N _0 e^{-\lambda t} $
Taking $\log$ both sides
$\ln |\frac{d N}{d t}|=\ln \left(\lambda N _0\right)-\lambda t$
Hence, $\ln |\frac{d N}{d t}|$ versus $t$ graph is a straight line with slope $-\lambda$.
From the graph we can see that, $\lambda=\frac{1}{2}=0.5 yr^{-1}$
Now applying the equation,
$ \begin{aligned} N & =N _0 e^{-\lambda t}=N _0 e^{-0.5 \times 4.16} \\ & =N _0 e^{-2.08}=0.125 N _0=\frac{N _0}{8} \end{aligned} $
i.e, nuclei decreases by a factor of $8$ .
Hence, the answer is $8$.





