Modern Physics Ques 47
- The radius of the orbit of an electron in a Hydrogen-like atom is $4.5 $ $a _0$ where $a _0$ is the Bohr radius. Its orbital angular momentum is $\frac{3 h}{2 \pi}$. It is given that $h$ is Planck constant and $R$ is Rydberg constant. The possible wavelength $(s)$, when the atom de-excites, is (are)
(2013 Adv.)
(a) $\frac{9}{32 R}$
(b) $\frac{9}{16 R}$
(c) $\frac{9}{5 R}$
(d) $\frac{4}{3 R}$
Show Answer
Answer:
Correct Answer: 47.(a,c)
Solution:
Formula:
Wavelength Corresponding To Spectral Lines:
- $L=3 (\frac{h}{2 \pi})$
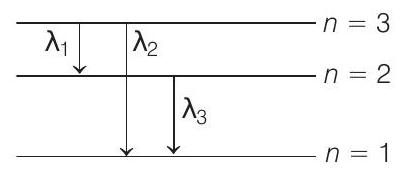
$ \begin{aligned} \therefore \quad & n=3, \text { as } L=n (\frac{h}{2 \pi}) \\ & r _n \propto \frac{n^{2}}{z} \\ & r _3=4.5 a _0 \\ \therefore \quad & z=2 \\ \therefore \quad & \frac{1}{\lambda _1}=R z^{2} \quad (\frac{1}{2^{2}}-\frac{1}{3^{2}})=4 R \quad (\frac{1}{4}-\frac{1}{9}) \\ \lambda _1 & =\frac{9}{5 R} \\ \frac{1}{\lambda _2} & =R z^{2} (\frac{1}{1^{2}}-\frac{1}{3^{2}})=4 R \quad (1-\frac{1}{9}) \\ \lambda _2 & =\frac{9}{32 R} \\ \Rightarrow \quad \frac{1}{\lambda _3} & =R z^{2} (\frac{1}{1^{2}}-\frac{1}{2^{2}})=4 R \quad (1-\frac{1}{4}) \\ \lambda _3 & =\frac{1}{3 R} \end{aligned} $





