Modern Physics Ques 70
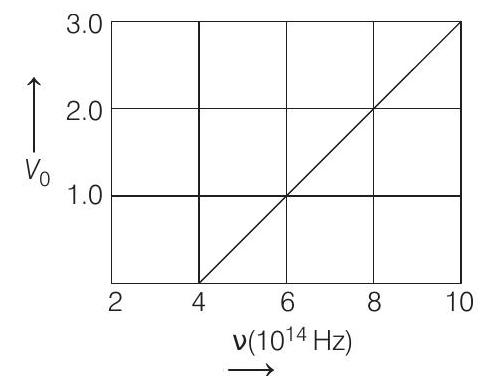
- The stopping potential $V _0$ (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be
(Take, Planck’s constant $(h)=6.63 \times 10^{-34} J$-s, electron charge, $e=1.6 \times 10^{-19} C$ ]
(Main 2019, 12 April I)
(a) $1.82 $ $eV$
(b) $1.66 $ $eV$
(c) $1.95 $ $eV$
(d) $2.12 $ $eV$
Show Answer
Answer:
Correct Answer: 70.(b)
Solution:
Formula:
- Given,
Planck’s constant,
$ \begin{aligned} h & =6.63 \times 10^{-34} J-s \\ e & =1.6 \times 10^{-19} C \end{aligned} $
and there is a graph between stopping potential and frequency.
We need to determine work function $W$.
Using Einstein’s relation of photoelectric effect,
$ \begin{aligned} (KE) _{\max } & =e V _0=h \nu-h v _0=h \nu-W \quad\left[\because W=h v _0\right] \\ V _0 & =\frac{h}{e} \nu-\frac{W}{e} \end{aligned} $
From graph at $V _0=0$ and $v=4 \times 10^{14} Hz$
$ \begin{aligned} & \therefore & 0 & =\frac{6.63 \times 10^{-34}}{e} \times 4 \times 10^{14}-\frac{W}{e} \\ & \Rightarrow & \frac{W}{e} & =\frac{6.63 \times 10^{-34} \times 4 \times 10^{14}}{e} J \end{aligned} $
$\text { or } W =6.63 \times 4 \times 10^{-20}$ $ J $
$\text { or } W =\frac{6.63 \times 4 \times 10^{-20}}{1.6 \times 10^{-19}} $ $eV=1.657 $ $eV $
$\therefore W =1.66 $ $eV$
Alternate Solution
From graph, threshold frequency,
$ v _0=4 \times 10^{14} Hz\left(\text { where, } V _0=0\right) $
$\therefore$ Work function, $W=h v _0$
$ \begin{array}{ll} \Rightarrow & W=6.63 \times 10^{-34} \times 4 \times 10^{14} J \\ \Rightarrow & W=\frac{6.63 \times 4 \times 10^{-20}}{1.6 \times 10^{-19}} eV=1.657 eV \approx 1.66 eV \end{array} $





