Modern Physics Ques 97
- Photoelectrons are emitted when $400 $ $nm$ radiation is incident on a surface of work function $1.9 $ $eV$. These photoelectrons pass through a region containing $\alpha$-particles. A maximum energy electron combines with an $\alpha$-particle to form a $He^{+}$ ion, emitting a single photon in this process. $He^{+}$ions thus formed are in their fourth excited state. Find the energies in $eV$ of the photons lying in the $2$ to $4 $ $eV$ range, that are likely to be emitted during and after the combination. [Take $h=4.14 \times 10^{-15} eV$-s]
(1999, 5M)
Show Answer
Answer:
Correct Answer: 97.During combination $3.4 $ $ eV$. After combination $3.84$ $ eV, 2.64$ $ eV$
Solution:
Formula:
- Given work function, $W=1.9$ $ eV$
Wavelength of incident light, $\lambda=400 $ $nm$
$\therefore$ Energy of incident light, $E=\frac{h c}{\lambda}=3.1 $ $eV$
(Substituting the values of $h, c$ and $\lambda$ )
Therefore, maximum kinetic energy of photoelectrons
$ K _{\max }=E-W=(3.1-1.9)=1.2 $ $eV $
Now the situation is as shown below :
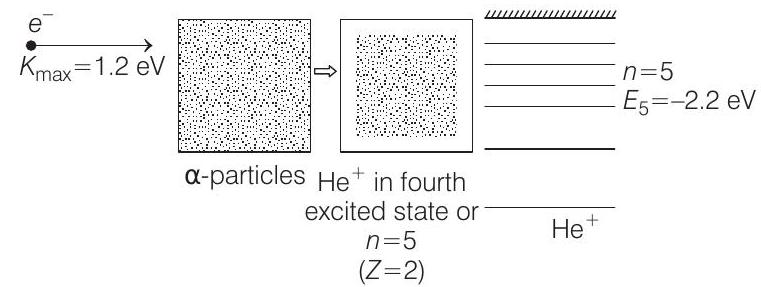
Energy of electron in $4^{\text {th }}$ excited state of $He^{+}(n=5)$ will be
$E _5=-13.6 \frac{Z^{2}}{n^{2}} eV \Rightarrow E _5=-(13.6) \frac{(2)^{2}}{(5)^{2}}=-2.2 $ $eV$
Therefore, energy released during the combination
$ =1.2-(-2.1)=3.4 $ $eV $
Similarly, energies in other energy states of $He^{+}$will be
$ \begin{aligned} & E _4=-13.6 \frac{(2)^{2}}{(4)^{2}}=-3.4 eV \\ & E _3=-13.6 \frac{(2)^{2}}{(3)^{2}}=-6.04 eV \\ & E _2=-13.6 \frac{(2)^{2}}{2^{2}}=-13.6 eV \end{aligned} $
The possible transitions are
$ \begin{aligned} \Delta E _{5 \rightarrow 4} & =E _5-E _4=1.2 eV<2 eV \\ \Delta E _{5 \rightarrow 3} & =E _5-E _3=3.84 eV \\ \Delta E _{5 \rightarrow 2} & =E _5-E _2=11.4 eV>4 eV \\ \Delta E _{4 \rightarrow 3} & =E _4-E _3=2.64 eV \\ \Delta E _{4 \rightarrow 2} & =E _4-E _2=10.2 eV>4 eV \end{aligned} $
Hence, the energy of emitted photons in the range of $2 $ $eV$ and $4 $ $eV$ are
$3.4 $ $eV$ during combination and
$3.84 $ $eV$ and $ 2.64$ after combination.





