Optics Ques 107
- A monochromatic beam of light is incident at $60^{\circ}$ on one face of an equilateral prism of refractive index $n$ and emerges from the opposite face making an angle $\theta(n)$ with the normal (see figure). For $n=\sqrt{3}$ the value of $\theta$ is $60^{\circ}$ and $\frac{d \theta}{d n}=m$. The value of $m$ is
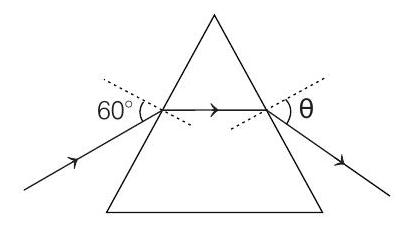
(2015 Adv.)
Show Answer
Answer:
Correct Answer: 107.$(2)$
Solution:
Formula:
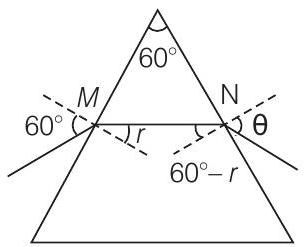
- Applying Snell’s law at $M$ and $N$,
$\sin 60^{\circ} =n \sin r $ $\quad$ …….(i)
$\sin \theta =n \sin (60-r)$ $\quad$ …….(ii)
Differentiating we get
$ \cos \theta \frac{d \theta}{d n}=-n \cos (60-r) \frac{d r}{d n} $ $+\sin (60-r)$
Differentiating Eq. (i),
$ \begin{aligned} & n \cos r \frac{d r}{d n}+\sin r=0 \\ & \text { or } \quad \frac{d r}{d n}=-\frac{\sin r}{n \cos r}=\frac{-\tan r}{n} \\ & \Rightarrow \quad \cos \theta \frac{d \theta}{d n}=-n \cos (60-r) (\frac{-\tan r}{n})+\sin (60-r) \\ & \frac{d \theta}{d n}=\frac{1}{\cos \theta}[\cos (60-r) \tan r+\sin (60-r)] \end{aligned} $
Form Eq. (i), $\quad r=30^{\circ}$ for $n=\sqrt{3}$
$\Rightarrow \frac{d \theta}{d n}=\frac{1}{\cos 60}(\cos 30 \times \tan 30+\sin 30)=2 (\frac{1}{2}+\frac{1}{2})=2$





