Optics Ques 110
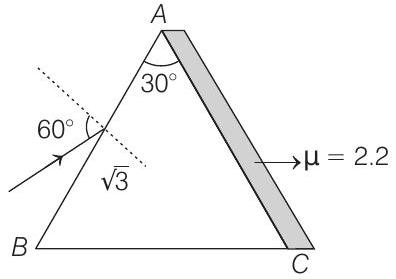
- A prism of refracting angle $30^{\circ}$ is coated with a thin film of transparent material of refractive index $2.2$ on face $A C$ of the prism. A light of wavelength $6600 \AA$ is incident on face $A B$ such that angle of incidence is $60^{\circ}$. Find
$(2003,4$ M)
(a) the angle of emergence and
(b) the minimum value of thickness of the coated film on the face $A C$ for which the light emerging from the face has maximum intensity. (Given refractive index of the material of the prism is $\sqrt{3}$ )
Show Answer
Answer:
Correct Answer: 110.(a) zero
(b) $1500 \AA$
Solution:
Formula:
- (a) $\sin i _1=\mu \sin r _1$
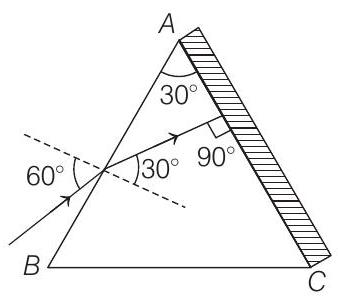
$\text { or } \sin 60^{\circ}=\sqrt{3} \sin r _1 $
$\therefore \quad \sin r _1 =\frac{1}{2} \text { or } r _1=30^{\circ} $
$ \text { Now, } r _1+r _2=A $
$\therefore \quad r _2 =A-r _1=30^{\circ}-30^{\circ}=0^{\circ}$
Therefore, ray of light falls normally on the face $A C$ and angle of emergence $i _2=0^{\circ}$.
(b) Multiple reflections occur between surface of film. Intensity will be maximum if constructive interference takes place in the transmitted wave.
For maximum thickness
$ \begin{aligned} \Delta x & =2 \mu t=\lambda \quad \quad(t=\text { thickness }) \\ \therefore \quad t & =\frac{\lambda}{2 \mu}=\frac{6600}{2 \times 2.2}=1500 \AA \end{aligned} $





