Optics Ques 111
- A prism of refractive index $n _1$ and another prism of refractive index $n _2$ are stuck together with a gap as shown in the figure. The angles of the prism are as shown. $n _1$ and $n _2$ depend on $\lambda$, the wavelength of
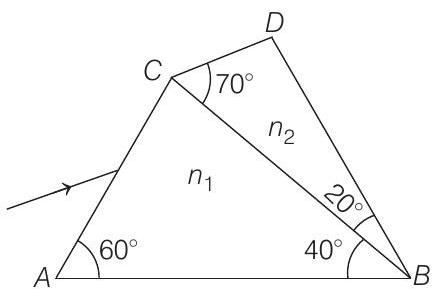light according to :
$ \begin{aligned} & n _1=1.20+\frac{10.8 \times 10^{4}}{\lambda^{2}} \text { and } \\ & n _2=1.45+\frac{1.80 \times 10^{4}}{\lambda^{2}} \end{aligned} $
where $\lambda$ is in $nm$.
(1998, 8M)
(a) Calculate the wavelength $\lambda _0$ for which rays incident at any angle on the interface $B C$ pass through without bending at that interface.
(b) For light of wavelength $\lambda _0$, find the angle of incidence $i$ on the face $A C$ such that the deviation produced by the combination of prisms is minimum.
Show Answer
Answer:
Correct Answer: 111.(a) $600$ $ nm$
(b) $\sin ^{-1} [\frac{3}{4}]$
Solution:
- $n _1=1.20+\frac{10.8 \times 10^{4}}{\lambda^{2}}$ and $n _2=1.45+\frac{1.80 \times 10^{4}}{\lambda^{2}}$
Here, $\lambda$ is in $nm$.
(a) The incident ray will not deviate at $B C$ if $n _1=n _2$
$
\begin{aligned}
& \Rightarrow 1.20+\frac{10.8 \times 10^{4}}{\lambda _0^{2}}=1.45+\frac{1.80 \times 10^{4}}{\lambda _0^{2}} \\
& \Rightarrow \quad \frac{9 \times 10^{4}}{\lambda _0^{2}}=0.25 \text { or } \lambda _0=\frac{3 \times 10^{2}}{0.5}
\end{aligned}
$
$
\lambda _0=600 $ $nm
$
(b) The given system is a part of an equilateral prism of prism angle $60^{\circ}$ as shown in figure.
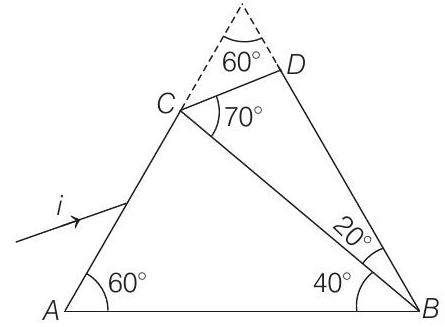
At minimum deviation,
$ r _1=r _2=\frac{60^{\circ}}{2}=30^{\circ}=r \text { (say) } $
$\therefore \quad n _1=\frac{\sin i}{\sin r} $
$\therefore \quad \sin i=n _1 \cdot \sin 30^{\circ} $
$\sin i=\{1.20+\frac{10.8 \times 10^{4}}{(600)^{2}} \}\quad (\frac{1}{2})=\frac{1.5}{2}=\frac{3}{4} $
$\text { or } \quad i=\sin ^{-1}(3 / 4)$
BETA
