Optics Ques 112
- A right angled prism $\left(45^{\circ}-90^{\circ}-45^{\circ}\right)$ of refractive index $n$ has a plane of refractive index $n _1\left(n _1<n\right)$ cemented to its diagonal face. The assembly is in air. The ray is incident on $A B$.
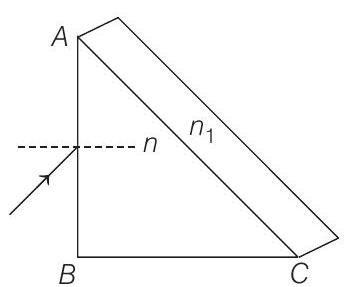
(1996, 3M)
(a) Calculate the angle of incidence at $A B$ for which the ray strikes the diagonal face at the critical angle.
(b) Assuming $n=1.352$, calculate the angle of incidence at $A B$ for which the refracted ray passes through the diagonal face undeviated.
Show Answer
Answer:
Correct Answer: 112.(a) $i _1=\sin ^{-1} \{\frac{1}{\sqrt{2}}\left(\sqrt{n^{2}-n _1^{2}}-n _1\right)\}$
(b) $ 73^{\circ} $
Solution:
Formula:
- (a) Critical angle $\theta _c$ at face $A C$ will be given by
$ \begin{aligned} \theta _c & =\sin ^{-1} (\frac{n _1}{n}) \\ \text { or } \quad \sin \theta _c & =\frac{n _1}{n} \end{aligned} $
Now, it is given that $r _2=\theta _c$
$ \therefore \quad r _1=A-r _2=\left(45^{\circ}-\theta _c\right) $
Applying Snell’s law at face $A B$, we have
$ \begin{aligned} & n=\frac{\sin i _1}{\sin r _1} \text { or } \sin i _1=n \sin r _1 \\ \therefore \quad i _1 & =\sin ^{-1}\left(n \sin r _1\right) \end{aligned} $
Substituting value of $r _1$, we get
$ \begin{aligned} i _1 & =\sin ^{-1}\{n \sin \left(45^{\circ}-\theta _c\right) \} \\ & =\sin ^{-1}\{n\left(\sin 45^{\circ} \cos \theta _c-\cos 45^{\circ} \sin \theta _c\right) \} \\ & =\sin ^{-1} \{\frac{n}{\sqrt{2}}(\sqrt{1-\sin ^{2} \theta _c}-\sin \theta _c)\} \\ & =\sin ^{-1} \{\frac{n}{\sqrt{2}} (\sqrt{1-\frac{n _1^{2}}{n^{2}}}-\frac{n _1}{n})\} \\ i _1 & =\sin ^{-1} \{\frac{1}{\sqrt{2}}(\sqrt{n^{2}-n _1^{2}}-n _1)\} \end{aligned} $
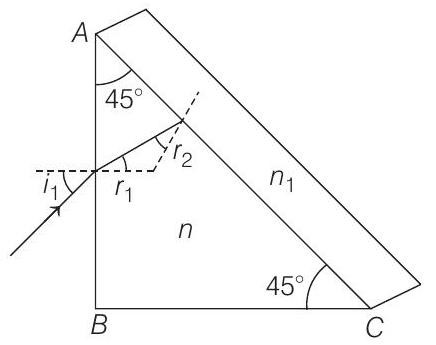
Therefore, required angle of incidence ( $\left.i _1\right)$ at face $A B$ for which the ray strikes at $A C$ at critical angle is
$ i _1=\sin ^{-1} \{\frac{1}{\sqrt{2}}\left(\sqrt{n^{2}-n _1^{2}}-n _1\right)\} $
(b) The ray will pass undeviated through face $A C$ when either $n _1=n$ or $r _2=0^{\circ}$ i.e. ray falls normally on face $A C$.
Here $n _1 \neq n$ (because $n _1<n$ is given )
$\therefore \quad r _2=0^{\circ}$
or $r _1=A-r _2=45^{\circ}-0^{\circ}=45^{\circ}$
Now applying Snell’s law at face $A B$, we have $n=\frac{\sin i _1}{\sin r _1}$
$\text { or } 1.352 =\frac{\sin i _1}{\sin 45^{\circ}}$
$\therefore \quad \sin i _1 =(1.352) (\frac{1}{\sqrt{2}}),$
$ \sin i _1 =0.956$
$ \therefore i _1 =\sin ^{-1}(0.956) \approx 73^{\circ}$
Therefore, required angle of incidence is
$ i=73^{\circ} $





