Optics Ques 116
- Monochromatic light is incident on a glass prism of angle $A$. If the refractive index of the material of the prism is $\mu$, a ray incident at an angle $\theta$, on the face $A B$ would get transmitted through the face $A C$ of the prism provided
(2015 Main)
(a) $\theta<\cos ^{-1} [ \mu \sin \{ A+\sin ^{-1} \frac{1}{\mu}\}]$
(b) $\theta<\sin ^{-1} [ \mu \sin \{ A-\sin ^{-1} \frac{1}{\mu}\}]$
(c) $\theta>\cos ^{-1} [ \mu \sin \{ A+\sin ^{-1} \frac{1}{\mu}\}]$
(d) $\theta>\sin ^{-1} [ \mu \sin \{ A-\sin ^{-1} \frac{1}{\mu}\}]$
Show Answer
Answer:
Correct Answer: 116.(d)
Solution:
Formula:
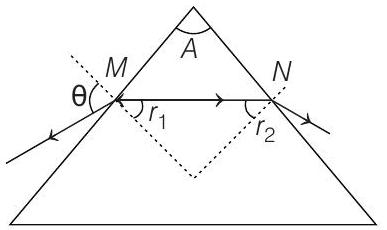
Applying Snell’s law at $M$,
$\mu=\frac{\sin \theta}{\sin r _1}$
$\therefore \quad r _1=\sin ^{-1} ( \frac{\sin \theta}{\mu} )\text { or } \sin r _1=\frac{\sin \theta}{\mu}$
Now, $\quad r _2=A-r _1=A-\sin ^{-1} (\frac{\sin \theta}{\mu})$
Ray of light would get transmitted form face $A C$ if
$ r _2<\theta _c \quad \text { or } \quad A-\sin ^{-1} (\frac{\sin \theta}{\mu})<\theta _c $
where,
$ \theta _c=\sin ^{-1} (\frac{1}{\mu}) $
$\therefore \quad \sin ^{-1} \frac{\sin \theta}{\mu}>A-\theta _c$
$\text { or } \frac{\sin \theta}{\mu}>\sin \left(A-\theta _c\right) $
$ \therefore \theta>\sin ^{-1}\left[\mu \sin \left(A-\theta _c\right)\right] $
$\text { or } \theta>\sin ^{-1} [\mu \sin \{A-\sin ^{-1} (\frac{1}{\mu})\}]$





