Optics Ques 136
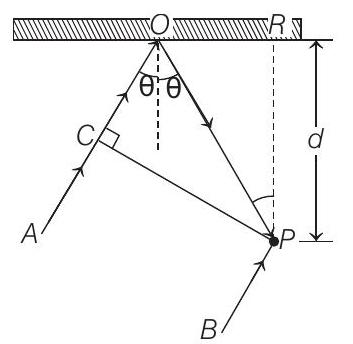
- In the adjacent diagram, $C P$ represents a wavefront and $A O$ and $B P$, the corresponding two rays. Find the condition of $\theta$ for constructive interference at $P$ between the ray $B P$ and reflected ray $O P$
$(2003,2 M)$
(a) $\cos \theta=\frac{3 \lambda}{2 d}$
(b) $\cos \theta=\frac{\lambda}{4 d}$
(c) $\sec \theta-\cos \theta=\frac{\lambda}{d}$
(d) $\sec \theta-\cos \theta=\frac{4 \lambda}{d}$
Show Answer
Answer:
Correct Answer: 136.(b)
Solution:
Formula:
- $P R=d$
$ \begin{array}{ll} \therefore & P O=d \sec \theta \\ \text { and } & C O=P O \cos 2 \theta=d \sec \theta \cos 2 \theta \end{array} $
path difference between the two rays is,
$ \Delta x=P O+O C=(d \sec \theta+d \sec \theta \cos 2 \theta) $
phase difference between the two rays is $\Delta \phi=\pi$ (one is reflected, while another is direct)
Therefore, condition for constructive interference should be
$ \Delta x=\frac{\lambda}{2}, \frac{3 \lambda}{2} \ldots $
or
$ d \sec \theta(1+\cos 2 \theta)=\frac{\lambda}{2} $
or
$ (\frac{d}{\cos \theta})\left(2 \cos ^{2} \theta\right)=\frac{\lambda}{2} \text { or } \cos \theta=\frac{\lambda}{4 d} $





