Optics Ques 157
- In an interference experiment, the ratio of amplitudes of coherent waves is $\frac{a _1}{a _2}=\frac{1}{3}$. The ratio of maximum and minimum intensities of fringes will be
(a) $2$
(b) $18$
(c) $ 4$
(d) $ 9$
(2019 Main, 8 April I)
Show Answer
Answer:
Correct Answer: 157.(c)
Solution:
Formula:
For Destructive interference :
- In Young’s double slit experiment, ratio of maxima and minima intensity is given by
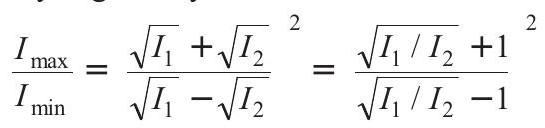
As, intensity $(I) \propto[\operatorname{amplitude}(a)]^{2}$
$\therefore \quad (\frac{I _1}{I _2})={(\frac{a _1}{a _2})}^{2}=\frac{1}{3}^{2}=\frac{1}{9}$
So, $\quad \frac{I _{\max }}{I _{\min }}=\left(\frac{\frac{1}{3}+1}{\frac{1}{3}-1}\right)^2=16: 1$





