Optics Ques 162
- A Young’s double slit interference arrangement with slits $S _1$ and $S _2$ is immersed in water (refractive index $=4 / 3$ ) as shown in the figure. The positions of maxima on the surface of water are given by $x^{2}=p^{2} m^{2} \lambda^{2}-d^{2}$, where $\lambda$ is the wavelength of light in air (refractive index $=1$ ), $2 $ $d$ is the separation between the slits and $m$ is an integer. The value of $p$ is
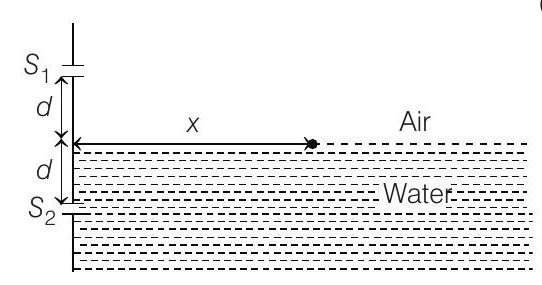
(2015 Adv.)
Show Answer
Answer:
Correct Answer: 162.$(3)$
Solution:
Formula:
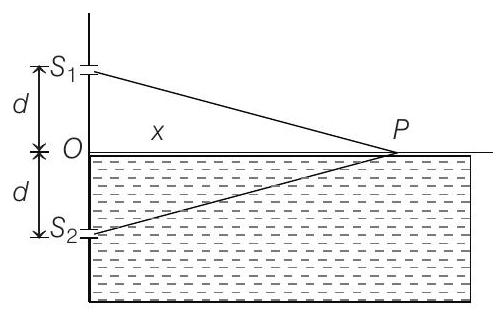
$ \begin{aligned} & \mu\left(S _2 P\right)-S _1 P=m \lambda \\ & \Rightarrow \quad \mu \sqrt{d^{2}+x^{2}}-\sqrt{d^{2}+x^{2}}=m \lambda \\ & \Rightarrow \quad(\mu-1) \sqrt{d^{2}+x^{2}}=m \lambda \\ & \Rightarrow \quad (\frac{4}{3}-1) \sqrt{d^{2}+x^{2}}=m \lambda \\ & \text { or } \quad \sqrt{d^{2}+x^{2}}=3 m \lambda \end{aligned} $
Squaring this equation we get,
$ \Rightarrow \quad x^{2} =9 m^{2} \lambda^{2}-d^{2}$
$\Rightarrow \quad p^{2}=9 \text { or } p=3$





