Optics Ques 170
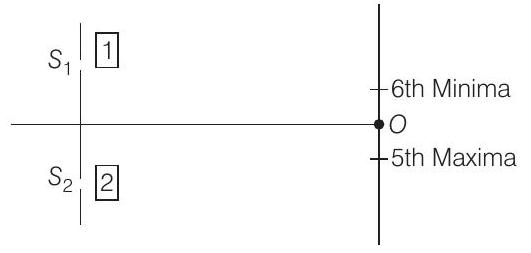
- In a Young’s experiment, the upper slit is covered by a thin glass plate of refractive index $1.4$, while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index $1.7$. Interference pattern is observed using light of wavelength $5400$ $ \AA$. It is found that the point $P$ on the screen, where the central maximum $(n=0)$ fall before the glass plates were inserted, now has $3 / 4$ the original intensity. It is further observed that what used to be the fifth maximum earlier lies below the point $P$ while the sixth minima lies above $P$. Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected).
$(1997,5$ M)
Show Answer
Answer:
Correct Answer: 170.$(9.3 $ $\mu m)$
Solution:
Formula:
- $\mu _1=1.4$ and $\mu _2=1.7$ and let $t$ be the thickness of each glass plates.
Path difference at $O$, due to insertion of glass plates will be
$ \Delta x=\left(\mu _2-\mu _1\right) t=(1.7-1.4) t=0.3$ $ t \quad …….(i) $
Now, since $5th$ maxima (earlier) lies below $O$ and 6th minima lies above $O$.
This path difference should lie between $5 \lambda$ and $5 \lambda+\frac{\lambda}{2}$
So, let
$ \Delta x=5 \lambda+\Delta \quad …….(ii) $
where
$ \Delta<\frac{\lambda}{2} $
Due to the path difference $\Delta x$, the phase difference at $O$ will be
$ \begin{aligned} \phi & =\frac{2 \pi}{\lambda} \Delta x=\frac{2 \pi}{\lambda}(5 \lambda+\Delta) \\ & =\left(10 \pi+\frac{2 \pi}{\lambda} \cdot \Delta\right) \quad …….(iii) \end{aligned} $
Intensity at $O$ is given $\frac{3}{4} I _{\max }$ and since
$ I(\phi)=I _{\max } \cos ^{2} (\frac{\phi}{2}) $
$\therefore \frac{3}{4} I _{\max } =I _{\max } \cos ^{2} (\frac{\phi}{2}) $
$ \text { or } \frac{3}{4} =\cos ^{2} (\frac{\phi}{2}) \quad …….(iv)$
From Eqs. (iii) and (iv), we find that
$ \begin{aligned} & \Delta=\frac{\lambda}{6} \\ \text { ie, } & \Delta x=5 \lambda+\frac{\lambda}{6}=\frac{31}{6} \lambda=0.3 t \\ \therefore & t=\frac{31 \lambda}{6(0.3)}=\frac{(31)\left(5400 \times 10^{-10}\right)}{1.8} \\ \text { or } & t=9.3 \times 10^{-6} m=9.3 \mu m \end{aligned} $





